Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Courbe paramétrée

Posté par
Pythix 11-04-07 à 18:35

Bonjour,
Voici mon exercice:
on considère la courbe
x(t)=\frac{t-sin(t)}{t^{2}}
y(t)=\frac{1-cos(t)}{t^{2}}

1) Détermnier le point limite quand t tend vers 0. OK (0,1/2)
2) Déterminer le vecteur dérivé et montrer que M est stationnaire ssi t=2tan(t/2). OK
3) Montrer que l'équation t/2=tan(t/2) admet une unique racine t_{n} dans ](2n-1)pi;(2n+1)pi[. OK

4) Préciser M(t_{n}).
5) Montrer que ces points stationnaires sont des points de rebroussement, qu'ils sont cocycliques et que les tangentes en ces points sont concourantes en un point que l'on précisera.
6) Donner l'allure du spupprot de la courbe.

Je ne vois pas pour les question 4) et 5)...
Merci d'avance pour toute aide.

Posté par
lafol Moderateurre : Courbe paramétrée 11-04-07 à 18:38

Bonjour
Question 4 : exprime sint et cost en fonction de tan(t/2) (alias t/2 pour t_n)

Posté par
Pythixre : Courbe paramétrée 11-04-07 à 18:44

c'est ce que j'ai fait pour la 3), il suffit de remplacer dans x et y?

Posté par
lafol Moderateurre : Courbe paramétrée 11-04-07 à 18:45

oui, et il devrait y avoir des simplifications

Posté par
Pythixre : Courbe paramétrée 11-04-07 à 18:46

ok, mais pour la 5) je vois pas du tout.

Posté par
lafol Moderateurre : Courbe paramétrée 11-04-07 à 18:51

pour montrer que ce sont des points de rebroussement, tu as du voir des critères sur la parité des premières dérivées non nulles ?
pour montrer qu'ils sont cocycliques, dis déjà ce que tu as trouvé, on verra.... et en même temps pour les tangentes concourantes ...

Posté par
Pythixre : Courbe paramétrée 13-04-07 à 10:57

j'ai trouvé x(t_{n})=y(t_{n})=\frac{1}{4}sin(t_{n})
mais pour le point de rebroussement, il faut faire un DL ?

Posté par
Pythixre : Courbe paramétrée 14-04-07 à 13:41

en fait je trouve:
x(t_{n})=\frac {1} {4} \sin(t_{n}) et y(t_{n})=\frac {1} {4}(1+cos(t_{n}))
j'avais repris l'expression de x(t)...
pour montrer que c'est un point de rebroussement, faut il se servir de DL ?

x(t_{n})=\frac{-1}{24}t_{n}^{3}+\frac{1}{4}t_{n}+o(t_{n}^{3})
y(t_{n})=\frac{1}{2}-\frac{1}{8}t_{n}^{2}+o(t_{n}^{3})

donc point de rebroussement normal tangent à (1/4,0) non ?

pour montrer qu'ils sont cocyliques, suffit il de dire que l'on reconnait la paramétrisation du cercle de centre (0,1/4) et de rayon 1/4 ?

Posté par
perroquetre : Courbe paramétrée 14-04-07 à 15:44

Bonjour, Pythix.

Tes expressions de x(t_n) et y(t_n) sont correctes. Et, effectivement, pour montrer qu'ils sont cocycliques, il suffit de dire qu'on reconnaît la paramétrisation du cercle de centre (0,1/4) et de rayon 1/4.

Par contre, tes dl sont incorrects (par exemple, t_n ne tend pas vers 0 ...). Il faut que tu reprennes les dérivées x'(t) et y'(t) et que tu calcules x''(t) et y''(t) (ainsi que les dérivées troisièmes, il n'y aura pas besoin d'aller plus loin): oui, ce n'est pas drôle ...).

On sait que x'(t_n)=y'(t_n)=0  ...

Posté par
lafol Moderateurre : Courbe paramétrée 14-04-07 à 16:00

Merci, perroquet, d'avoir pris la relève en mon absence. je te laisse la main....

Posté par
Pythixre : Courbe paramétrée 14-04-07 à 18:31

oui c'est assez lourd, on ne peut pas faire le dl en posant t=t_n+h ?

Posté par
perroquetre : Courbe paramétrée 14-04-07 à 21:44

C'est possible, mais attention, il faut le faire avec
x(t)={t-\sin t \over t^2}\qquad y(t)={1-\cos t\over t}

Posté par
Pythixre : Courbe paramétrée 14-04-07 à 23:31

oui mais on va avoir du sin(tn) et du cos(tn) qui va apparaitre non ?

Posté par
patrice rabillerre : Courbe paramétrée 15-04-07 à 05:59

Comme le disait perroquet plus haut, il faut calculer x''(t) et y''(t).

Pour ma part j'ai trouvé :

4$x''(t)=\frac{4t\cos t+t^2\sin t-6\sin t+2t}{t^4}
4$y''(t)=\frac{-4t\sin t+t^2\cos t+6-6\cos t}{t^4}

Si on calcule ce vecteur pour t=tn, on obtient, sauf erreur :

4$x''(t_n)=\frac{6(t_n^2-4)}{t_n^3\(t_n^2+4\)}
4$y''(t_n)=\frac{-16-t_n^2}{t_n^2\(4+t_n^2\)}

En effet, puisqu'on sait que 4$t_n=2\tan\(\frac{t_n}{2}\),
on peut en déduire que : 4$\cos(t_n)=\frac{4-t_n^2}{4+t_n^2} et que 4$\sin (t_n)=\frac{8t_n}{4+t_n^2}.

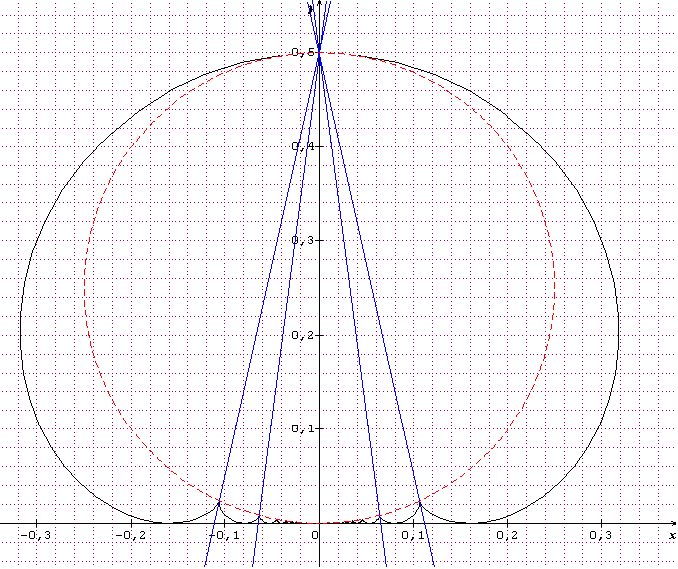
Graphiquement, les points stationnaires sont bien des points de rebroussement appartenant au cercle de centre (0;0,25) et de rayon 0,25 et les tangentes aux points de rebroussement sont concourrantes au point (0;0,5).

J'ai dessiné ci-dessous les tangentes aux premiers points de rebroussement (t18,987 et t215,45).

Je n'ai pas eu le courage de calculer les dérivées d'ordre 3 ...

Courbe paramétrée

Posté par
Pythixre : Courbe paramétrée 15-04-07 à 11:07

merci beaucoup de votre aide!

je ne connaissait pas ces formules comme ca...
mais comment prouve t on que les tangentes sont bien concourantes ?

Posté par
patrice rabillerre : Courbe paramétrée 15-04-07 à 11:38

Pour montrer que les tangentes sont concourrantes, c'est maintenant assez facile (si on peut dire) car on connaît le vecteur directeur de ces tangentes (sauf si j'ai fait des erreurs de calcul).

Ainsil les points stationnaires (et de rebroussement mais ce n'est pas encore démontré), ont pour coordonnées \(\frac 1 4\sin t_n;\frac 1 4(1+\cos t_n)\)

À partir de là si on parvient à écrire l'équation des tangentes aux points M(tn) sous la forme y=ax+b avec b=0,5, indépendant de tn, alors ce sera gagné...

Posté par
Pythixre : Courbe paramétrée 15-04-07 à 11:45

on a vu les des points de rebroussement qu'avec un DL...

Posté par
patrice rabillerre : Courbe paramétrée 15-04-07 à 12:08

Peut-être, mais les DL sont difficiles à utiliser ici... Il faut plutôt se tourner du côté de la parité des premières dérivées comme l'a dit plus haut lafol.

Posté par
Pythixre : Courbe paramétrée 15-04-07 à 12:42

je viens de regarder mon cours mais pas de critère avec la parité des dérivées...

Posté par
patrice rabillerre : Courbe paramétrée 15-04-07 à 15:57

Il y a peut être un moyen plus simple pour déterminer les points de rebroussements :

Les racines tn qui annulent x'(t) et y'(t) sont certainement des racines simples (ce n'est qu'une intuition). Dans ce cas, pour chaque valeur de tn, x'(t) et y'(t) changent tous deux de signes. On peut alors en conclure qu'il s'agit bien de points de rebroussement.

Je sais : ce raisonnement n'est pas très rigoureux ... mais c'est tout ce que j'ai pour lme moment

Posté par
Pythixre : Courbe paramétrée 15-04-07 à 16:08

je ne comprends pas comment vous trouvez les formules avec cos(tn) et sin (tn) en fonction de tn...

Posté par
perroquetre : Courbe paramétrée 15-04-07 à 16:09

Bonjour, Pythix.

Patrice rabiller a bien fait avancer les choses. Pour répondre à ton problème:
x(t_n+h)=x(t_n)+hx'(t_n)+h^2/2x''(t_n)+h^3/6x'''(t_n)+o(h^3)
y(t_n+h)=y(t_n)+hy'(t_n)+h^2/2y''(t_n)+h^3/6x'''(t_n)+o(h^3)

Donc:
(x_(t_n+h),y(t_n+h))= (x(t_n),y(t_n)) + h^2/2(x''t_n),y''(t_n))
+h^3/6 (x'''(t_n),y'''(t_n)) + o(h^3)

Tu as maintenant tes DL (en supposant résolu le problème de la dérivée troisième).

La tangente en M(t_n) est maintenant dirigée par (x''(t_n),y''(t_n))

Posté par
patrice rabillerre : Courbe paramétrée 15-04-07 à 18:01

Pour répondre à Pythix concernant les formules avec cos(tn) et sin(tn), voici l'explication :

On sait que, pour tout réel x : cos(2x)=2cos2x-1=1-2sin2x.

On en déduit : \cos^2 x=\frac{1+\cos{2x}}{2} et \sin^2 x=\frac{1-\cos{2x}}{2}

Donc \tan^2x=\frac{\sin^2 x}{\cos^2 x}=\frac{1-\cos{2x}}{1+\cos{2x}}

On en déduit : \cos{2x}=\frac{1-\tan^2 x}{1+\tan^2 x}

Donc, en posant x=tan(t/2), on obtient : \cos x=\frac{1-t^2}{1+t^2}

De plus, lorsque t=tn, alors on a tn/2=tan(tn/2)

On en déduit : 4$\cos(t_n)=\frac{1-\tan^2\(\frac{t_n}{2}\)}{1+\tan^2\(\frac{t_n}{2}\)}=\frac{1-\frac{t_n^2}{4}}{1+\frac{t_n^2}{4}}=\frac{4-t_n^2}{4+t_n^2}

Un raisonnement analogue conduit à la formule que j'ai donnée pour sin(tn)

Posté par
Pythixre : Courbe paramétrée 15-04-07 à 18:37

Un grand merci, ca aura été labourieux...


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !