Inscription / Connexion Nouveau Sujet
Courbe paramétrée
Bonjour à tous!
Je n'arrive pas à résoudre cet exercice, pouvez vous m'aider?
Voici l'énoncé:
Le but de cet exercice est de tracer, dans un repère orthonormé du plan, la courbe paramétrée C définie par: M(t)= (x(t)= cos(3t); y(t)= sin(2t)) pour tout t 
 .
.
1)Montrer que cette courbe est incluse dans un carré du plan que vous préciserez.
2)Montrer que pour tout t 
 , M(t+2
, M(t+2 )= M(t). En quoi cette relation est-elle intéressante pour l'étude de C?
)= M(t). En quoi cette relation est-elle intéressante pour l'étude de C?
3)Etudier la parité de x(t) et de y(t). Quelle propriété de C peut-on en déduire?
4)Exprimer x( -t) et y(
-t) et y( -t) en fonction de x(t) et de y(t) (ces propriétés permettent d'affirmer que la courbe C est symétrique par rapport à l'origine.
-t) en fonction de x(t) et de y(t) (ces propriétés permettent d'affirmer que la courbe C est symétrique par rapport à l'origine.
5)
a)Etudier les fonctions x(t) et y(t) sur l'intervalle [0; /2].
/2].
b)Determiner la position du point M lorsque t= 0, /6,
/6, /4,
/4, /3 et
/3 et  /2.
/2.
c)Determiner le coefficient directeur de la tangente à C aux points M( /6) et M(
/6) et M( /2).
/2).
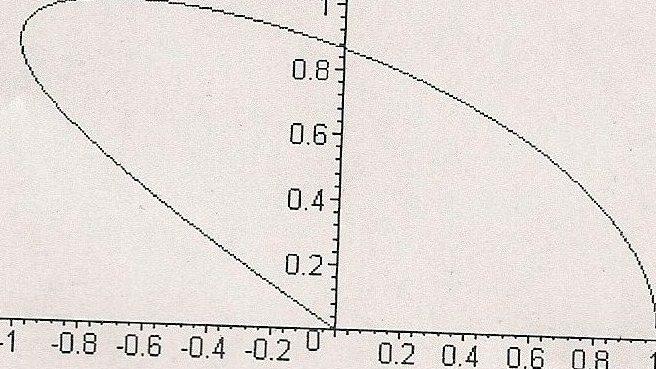
6) Une partie de la courbe C obtenue pour t  [0;
[0; /2] vous est fournie ci dessous. Tracer la courbe complète de C en justifiant votre construction et en faisant figurer toutes les informations relatives aux questions 5b et 5c.
/2] vous est fournie ci dessous. Tracer la courbe complète de C en justifiant votre construction et en faisant figurer toutes les informations relatives aux questions 5b et 5c.
Alors pouvez m'aider s.v.p.
Je n'ai pas d'éléments de réponses car je n'arrive pas à débuter.
Bonsoir,
1) Pour la question 1 on te demande en fait de borner x(t) et y(t). Comme tu vas trouver les mêmes bornes pour x et y tu vas en déduire un "carré" du plan dans lequel toute ta courbe sera comprise
2) Le fait que tes fonction x et y soient périodique te permet de les étudier sur un petit intervalle au lieu de tout R
3) Tu déduis des parités de x et y certains axes de symétrie pour ta courbe. Ainsi tu pourras encore réduire l'intervalle d'étude : il te suffira de connaitre les variation de x et y sur un intervalle plus petit puis de compléter en sachant qu'une fonction paire est symétrique par rapport à l'axe des ordonnées et ...
Ça devrait t'aider à débuter, nous t'aiderons pour les dernières questions au besoin.
Bon courage.
Grillé 
N'as-tu aucun exemple d'étude de courbe paramétrée dont tu puisses t'inspirer (cours, livre d'exos) ? C'est vraiment du classique.
Bonsoir, je ne sais pas j'ai toutes les réponses, mais voilà ce que je peut te donner :
1)Montrer que cette courbe est incluse dans un carré du plan que vous préciserez:
pour ma part je dirai que le carré en question est le carré centré en 0 et avec 2 "pour la longueur des cotés". En effet, x=cos(3t) et y=sin(2t), on peut donc dire que et
, autrement dit, ton dessin appartient à l'ensemble suivant :
...et cet ensemble correspond bien au carré centré en 0 avec "pour longueur des cotés" : 2 .
2)2)Montrer que pour tout t , M(t+2)= M(t). En quoi cette relation est-elle intéressante pour l'étude de C.
Cette question est classique lorsque tu étudies un arc paramétré de ce type (c'est à dire avec des x et y étant des fonctions périodique).L'intérêt de cette question est de restreindre le domaine d'étude de ta fonction, histoire de simplifier les calculs car parfois il suffit de connaitre comment "marche" ton arc sur un certain intervalle pour savoir comment il "marche" sur son intervalle de définition tout entier.Justement, c'est le cas ici,en effet, pour (x(t)= cos(3t) et y(t)= sin(2t) on a que , donc pour étudier x et y tu dois l'étudier sur
...or prendre
n'est pas très pratique car il y'a plein de cas à vérifier...on peut donc ici restreindre le domaine d'étude de ton arc à un intervalle de longueur 2Pi puisque M(t+2Pi)=M(t).
En effet, . Donc " M est 2-périodique " donc connaitre M sur un intervalle de longueur
équivaut à connaitre M sur
tout entier. Ainsi on peut prendre t appartenant à un intervalle de longueur
, par exemple l'intervalle
(on prend généralement cet intervalle car il est symétrique....ce qui arrange bien les choses si l'on veut continuer à restreindre le domaine d'étude (justement, l'on va faire cela dans tes question 3 et 4).
3)Étudier la parité de x(t) et de y(t). Quelle propriété de C peut-on en déduire?
x(-t)=cos(-3t)=cos(3t)=x(t) et y(-t)=-y(t). On peut en déduire que C admet l'axe des abscisses (ie y=0) comme axe de symétrie. Et donc tu peux restreindre ton intervalle d'étude à l'intervalle ...donc tu obtiendra le dessin de C pour t appartenant à
, et pour avoir l'allure de C sur
il te suffira de dessiner le symétrique de ce que tu auras selon l'axe Ox.
4)Exprimer x(Pi-t) et y(Pi-t) en fonction de x(t) et de y(t) (ces propriétés permettent d'affirmer que la courbe C est symétrique par rapport à l'origine.
et
(je ne détaille pas cela.)
D'où la symétrie par rapport à l'origine. Et donc l'on peut prendre t dans l'intervalle puis l'on (enfin tu) fera une symétrie par rapport à l'origine de ce que tu obtiendra en étudiant C sur
.
5)
a)Etudier les fonctions x(t) et y(t) sur l'intervalle
Bon là ça deviens sordide à taper en Latex...et puis il commence à ce faire tard alors je dis comment procéder en essayant d'être le plus claire possible: Tu va donc d'après les questions 2) 3) 4) étudier C, ie M ie x et y sur l'intervalle . Donc d'abord, tu dérives x, puis y et tu va étudier le signe des dérivées donc les variations de x et y ensuite. Dans la pratique on met toutes ces informations dans un tableau de variation mais avec 4 lignes : première et troisième lignes pour le signe de x' et y' et deuxième et quatrième lignes pour les variations de x et de y...et en fait il y'a une autre ligne forcément qui est au dessus de autres qui correspond à l'intervalle auquel appartient t(ici:
). Celà permet de voir simultanément les variations de x et de y en même temps.C'est plus pratique

b)Determiner la position du point M lorsque t= 0,pi/6,pi/4,pi/3 et
Bon ben tu remplace t par les valeurs qui te sont données.
c)Determiner le coefficient directeur de la tangente à C aux points M(/6) et :
Je te montre : il faut considérer le vecteur
si je ne m'abuse...et ce vecteur est le coefficient directeur de la tangente au point
(J'ai un petit doute du coup....mais je dirais que cela...si quelqu'un pense que c'est faux qu'il me corrige merci
 )
)
Et ensuite, si ce que te dis est bien vrai, tu feras de même pour ton autre point.
6) Une partie de la courbe C obtenue pour t [0;/2] vous est fournie ci dessous. Tracer la courbe complète de C en justifiant votre construction et en faisant figurer toutes les informations relatives aux questions 5b et 5c.
Bon ben tu places tout tes points, tu regardes ton joli tableau de variation à double entrée, tu fais les deux symétries précédemment citées et hopppe le tour est joué....et moi je vais aller me coucher
En espérant t'avoir aidé  et surtout en espérant avoir été clair
et surtout en espérant avoir été clair 
au fait, je viens d'y penser il y'a 5 minutes, mais un joli by maple te parlera peu être un plus, et te permettra de mieux cerner l'histoire des deux symétries. Les vois-tu sur le dessins ci-dessous?
Bon, je ne vois pas quoi dire de plus sinon que tu peux essayer de t'entrainer dans des livres, c'est au programme des classes préparatoires genre MPSI,PCSI,... il me semble...donc dans des ouvrages du genre le Monier etc... tu devrais pouvoir trouver pas mal d'exercices pour t'entrainer, car ce n'est pas vraiment compliqué ce type d'exercice....mais ça demande quand même pas mal d'entrainement. Alé bonne soirée/nuit et si des questions persistent, surtout n'hésite pas !
En espérant que tu a pu compléter l'exercice grâce à l'aide d'Olivski, je te conseille de conserver et revoir le cas échéant cet exercice en tant que "modèle" de base pouvant t'aider à résoudre d'autres exercices du genre sur les mêmes principes. Auras-tu un corrigé en cours ou as-tu cherché cet exercice de ta propre initiative ?


 géométrie en post-bac
géométrie en post-bac