Inscription / Connexion Nouveau Sujet
Courbe paramétrée
Bonjour,
Soit C : { x(t)=cos(t) , y(t)=sin(t) } qui définie le cercle unité centré sur O.
1) Determiner l'équation de la tangente Tt à C au point M(t)(cost,sint) en fonction de t.
2) Donner, en fonction de t, les cordonnées de A(t) et B(t) les intersections respectives de C avec l'axe Ox et Oy, soit I(t) le milieu de [A(t)B(t)]. Déterminer l'équation cartésienne de la courbe décrite par I(t) lorsque t varie.
Au début je sens bien que le vecteur tangent est M'(t)(-sint,cost) mais comment obtenir l'équation ?
Après il faut résoudre { C inter x=0 } et { C inter y=0 } mais ceci nous enlève les t , car on sait bien que les point A(t) et B(t) on pour coordonnées respectifs (1,0);(-1,0) et (0,1);(0,-1)
merci de m'aider
Bonsoir,
mais comment obtenir l'équation ?
Une droite de vecteur normal
car on sait bien que les point A(t) et B(t) on pour coordonnées respectifs (1,0);(-1,0) et (0,1);(0,-1)
Ben non...
Un dessin:
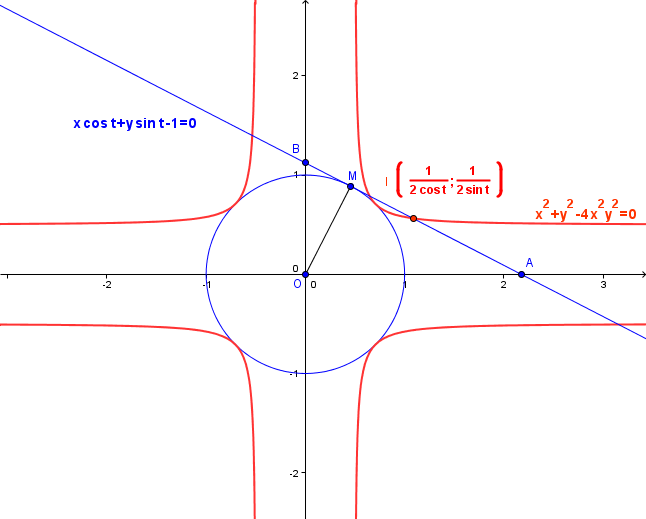

On a
Imaginons qu'on ait le point
Alors les vecteurs et
sont orthogonaux.
Donc
Soit
Pour la deuxième question, ton énoncé n'est pas clair, est-ce que et
ne seraient pas plutôt les intersections de
avec les axes ?
Oui tu as raison ! c'est bien une faute de l'énoncé !
l'équation de la tangente au point M(t) est donc :
y= -(cost/sint)x +(1/sint)
ensuite A(t) à pour coordonnée (1/cost , 0 )
B(t) ( 0 , 1/sint)
I(t) à pour coordonnée ( 1/2cost ; 1/2sint )
qui fournit l'équation cartésienne : x^2 + y^2 -4x^2y^2=0
La suite de l'énoncé demandé justement l'étude de la courbe { x(t) = 1/2cos(t) et y(t)=1/2sin(t) }
Merci beaucoup


 géométrie en post-bac
géométrie en post-bac