Inscription / Connexion Nouveau Sujet
Courbe paramétrée: représentation graphique
Bonjour,
Cela fait 2 jours que je suis sur le graphe de la courbe paramétrée selon:
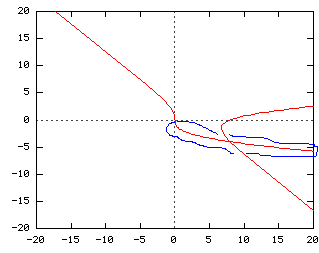
Je ne parviens pas à obtenir la "bonne courbe" que le prof m'a montrée, à savoir celle en pièce jointe.
Je m'explique.
A partir de l'étude des différentes branches paraboliques et autres tangentes et asymptotes, je trouve déjà qu'il faut tracer l'asymptote oblique d'équation . Elle n'est pas tracée sur le graphe joint, mais on la devine aisément.
La partie du graphe que je ne parviens pas à comprendre est située de à
pour les
et de
à
pour les
(sur la partie positive de l'axe des abscisses, la courbe en prolongement de celle à gauche des abscisses ... je suis clair?
 >> partie etourée en bleu!)
>> partie etourée en bleu!)
Ainsi donc, je ne comprends pas pourquoi cette portion de graphe, à partir de mon tableau de variations, est dirigée comme cela, et ne suis pas plutôt l'asymptote oblique , et ne couperait donc pas l'autre partie du graphe!
Pouvez-vous m'expliquer?
Merci d'avance.
Bonjour matix
La courbe que ton prof a donnée est la bonne.
L'asymptote oblique d'équation y=-x+3 correspond aux 2 branches infinies lorsque t 1-, (au nord ouest) et lorsque t
1-, (au nord ouest) et lorsque t 1+ (au sud est).
1+ (au sud est).
Lorsque t -
- et lorsque t
et lorsque t +
+ , la courbe présente une branche parabolique d'axe Ox : il suffit de regarder la limite du rapport y/x qui tend vers 0 lorsque t tend vers
, la courbe présente une branche parabolique d'axe Ox : il suffit de regarder la limite du rapport y/x qui tend vers 0 lorsque t tend vers 
 .
.
Voilà, j'espère que ça va t'aider.
Merci de votre réponse 
Malheureusement, je ne comprends pas davantage. Je suis tout à fait d'accord avec tout ce que vous me dîtes, je l'avais trouvé auparavant; cependant, je ne vois en quoi cela répond à ma question concernant la direction que prend la courbe au niveau entouré en bleu: Pourquoi ce ce côté elle ne tend pas vers l'asymptote alors qu'à gauche elle le fait?
Bonjour matix
La différence fondamentale est que dans le premier cas, il s'agit bel et bien d'une asymptote, alors que dans le deuxième cas, c'est une branche parabolique de direction Ox (comme l'a dit patrice rabiller) et là justement, la courbe s'éloigne de l'axe.
Kaiser
Ok kaiser! Alors, je ne sais pas si patrice rabiller l'a indiqué, ou alors je n'ai pas saisi, mais pourquoi dans le premier cas c'est bien une asymptote et pas dans l'autre?
Pour qu'il y ait asymptote, il faut le rapport tende vers une limite finie que l'on note m et
tende vers une limite finie p auquel cas la droite d'équation y=mx+p est asymptote à la courbe.
Dans le deuxième cas le rapport tend vers 0 mais y(t) tend vers
ce qui signifie que |x(t)| croit plus vite que |y(t)|, d'où l'allure de la courbe.
Je vais reprendre tout cela doucement ... Mais pouvez-vous m'indiquer clairement et concrètement comment on doit représenter une branche parabolique?
C'est à dire que pour une branche parabolique de direction par exemple, la courbe doit s'éloigner de
?


 géométrie en post-bac
géométrie en post-bac