Inscription / Connexion Nouveau Sujet
courbes parametrées
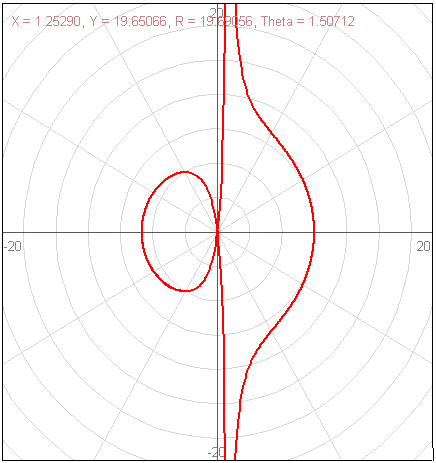
bonjour à tous j'ais un gros probleme pour faire la representation graphique de la courbe definie par x(t)=1+8cos(t)
y(t)=tan(t)+8sin(t)
j'ais trouver x(-t)=x(t)
y(-t)=-y(t) d'ou une symetrie/(ox)
x'(t)=-8sin(t)
y'(t)=1/cos^2(t)+8cos(t)
lim(-pi/2)y(t)=lim(3pi/2)=1 sachant que t decrit ]-pi/2;pi/2[U]pi/2;3pi/2[
merci de m'aider essentiellement pour la representation graphique(meme à la calculatrice je ne vois pas bien ce qu'il se passe,c'est pourquoi je vous demande votre aide)

L'étude de cette fonction ne présente rien d'exceptionnel.
On peut même la mettre sous la forme :
y(x) = (+ou-) x*racine((64/(x-1)²)-1)
mais ce n'est probablement pas ce qui est souhaité.
salu à tous et merci à JJa.Dans ce meme exercice,j'ais encore un probleme,on me demande de donner les coordonées d'un vecteur normal en un point quelconque de la droite.E ca je ne sais absolument pas faire,si quelqu'un pouvait me donner la methode avec un exemple ca m'aiderait vachement.Je vous en remerci par avance.
Par ailleurs,il faut donner une equation polaire de cette courbe:j'ais penser que  =
= (x^2+y^2) mais pour le teta je sais pas non plus comment faire.
(x^2+y^2) mais pour le teta je sais pas non plus comment faire.
Je remerci d'avance toute les personnes qui pourront m'aider à ce sujet.

Bonjour
en écrivant r²=x²+y² et en remplaçant, tu arrives à r=8+1/cost
(fais apparâitre de carrés pour pouvoir simplifier ton r² en r)
Philoux
salut philoux c'est sympa de me repondre mais je ne vois pas comment tu trouve ton r=8+1/cos(t):
x^2+y^2=(1+8cos(t))^2+(tan(t)+8sin(t))^2
=(aprés simplification)16/cos(t)+65+tan^2(t)
je vois pas comment tu trouves ce resultat.
Merci de m'aider et de m'eclaircir.


En ce qui concerne le vecteur normal;si l'on cherche à M(pi/6):
x'(pi/6)=-8sin(pi/6)=-4
y'(pi/6)=4/3 +4 2
2
je sais qu'il fo commencer par faire ces calculs mais je ne rappelle plus comment on fait la suite,si quelqu'un pouvait m'aider se serait sympa.Merci d'avance.






 géométrie en post-bac
géométrie en post-bac