Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Courbes Paramétrées du plan

Posté par
Berry 24-05-10 à 16:50

Bonjour, bonjour

Je vous explique mon problème : je sèche depuis plusieurs heures sur un exercice de mini projet de maths... =S
Et cela dès les premières questions, et sachant qu'il y en a une dizaine qui suivent, je suis pas sortie de l'auberge.
Alors, alors, l'énoncé !!

Soient R +* , ]0,1[ , r = R. On se donne, dans le plan, un repère orthonormé direct R = (O,,) et on considère le point A(R,0), le cercle C de centre O et de rayon R, le cercle centrée en sur la demi-droite [O,), de rayon r, tangent intérieurement à C en A.
Pour tout t , on considère le c ercle (t) centré en (t) sur la demi-droi d'angle polaire t ( c'est à dire que l'angle orienté (, O(t)) = t[2]), de rayon r, et tangent à C intérieurement au point C(t).

On fait rouler sans glisser le cercle à l'intérieur du cercle fixé C en supposant qu'il coïncide à l'instant t avec le cercle (t). On note M(t) le point de à l'instant t (donc de (t)) qui est en A à l'instant 0.

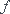
Le but du problème est d'étudier l'arc paramétré C() = (,, H()) représentant la trajectoire (H()) du point M(t)(OM(t) = f(t)) dans le repère R = (O,,).

1. Préciser la longueur commune des arcs M(t)C(t) du cercle (t) et AC(t) du cercle C.
2. En déduire des mesures des angles orientés ((t)M(t),(t)C(t)) et (,(t)M(t)) en fonction de t.
3. Déterminer les coordonnées des point C(t) et (t) dans le repère orthonormé direct R.


Déjà, ces trois premières questions me posent problème. Je n'ai aucune idée de la marche à suivre étant donné que pour seul support j'ai un polycopié de 10 pages de cours...

Si quelqu'un pourrait me guider, cela serait vraiment génial

PS : je ne sais pas comment faire les vecteurs donc si des expressions paraissent incompréhensibles, c'est à cause de ça.

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 24-05-10 à 18:25

Bonjour,

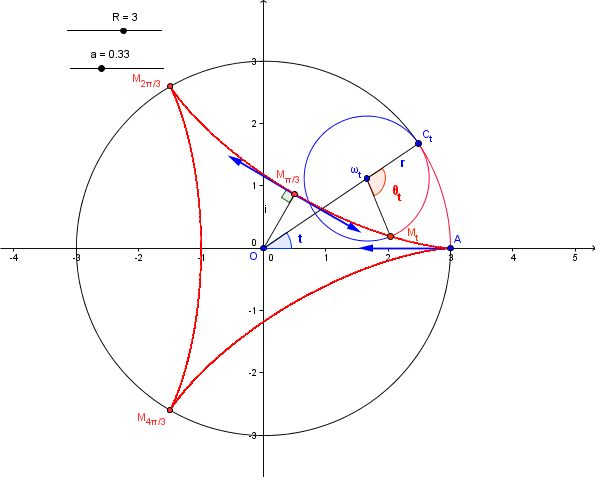
Un dessin pour débuter:

Courbes Paramétrées du plan

Il faut exprimer \theta en fonction de t sachant que les deux arcs en rouge sont de longueur égales.

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 24-05-10 à 20:28

1) En appelant \ell cette longueur communne et \theta_t=(\vec{\omega M_t},\vec{\omega C_t}):

\ell= Rt=r\theta _t=\alpha R \theta_t

2) On en déduit:

(\vec{\omega M_t},\vec{\omega C_t})=\theta_t=\frac{t}{\alpha}

Puis:

(\vec{i}\vec{\omega_t M_t})=(\vec{i},\vec{\omega_tC_t})+(\vec{\omega C_t},\vec{\omega_tM_t})\;\;[2\pi]

(\vec{i}\vec{\omega_t M_t})=t-\theta_t=\frac{\alpha -1}{\alpha}t\;\;[2\pi]

3) C_t\|R\,\cos\,t\\R\,\sin\,t

\omega_t\|R(1-\alpha)\,\cos\,t\\R(1-\alpha)\,\sin\,t

Pour la suite, c' est à dire les coordonnées de M_t\|X\\Y:

\vec{OM_t}=\vec{O\omega_t}+\vec{\omega_tM_t}

On obtient:

\{X=R\left[(1-\alpha)\,\cos\,t+\alpha\,\cos\,\left(\frac{1-\alpha}{\alpha}t\right)\right]\\Y=R\left[(1-\alpha)\,\sin\,t-\alpha\,\sin\,\left(\frac{1-\alpha}{\alpha}t\right)\right]

Voici ce que ça donne avec \alpha=\frac{1}{5}

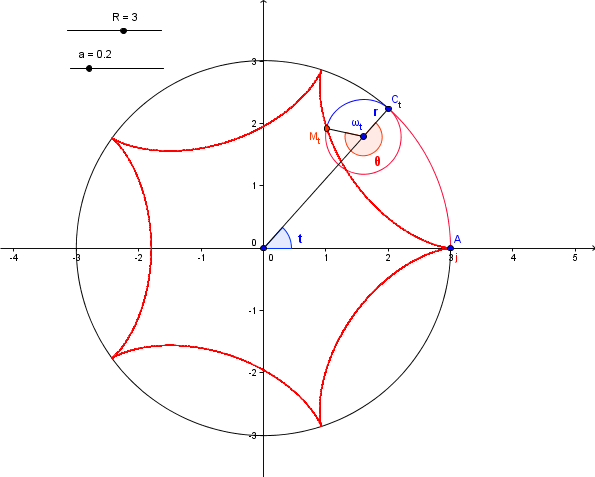
Courbes Paramétrées du plan

Ou \alpha=0.24 par exemple:

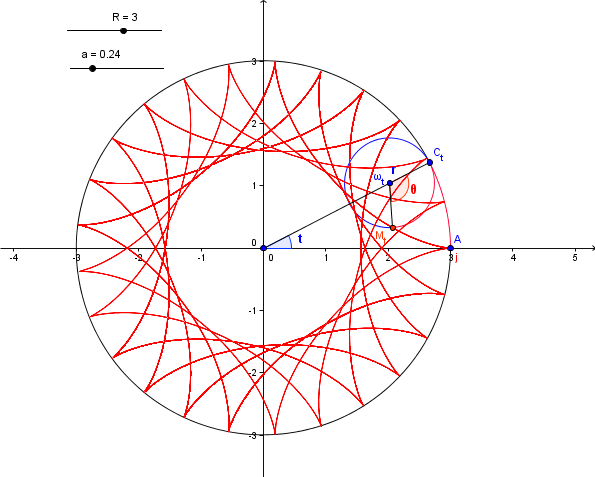
Courbes Paramétrées du plan




Posté par
infophilere : Courbes Paramétrées du plan 24-05-10 à 21:22

Joliii

Posté par
Berryre : Courbes Paramétrées du plan 24-05-10 à 21:23

Je comprends, en fait les schémas aident vraiment beaucoup, parce que j'avais vraiment du mal à visualiser.
Vous avez fait cela avec Géogebra ?

L'exercice n'est pas finis, mais je vais essayer de trouver la suite par moi même, avant de redemander de l'aide

En tout cas, merci beaucoup, vous m'avez bien débloquée =)

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 24-05-10 à 22:04

>> Berry Oui, Geogebra.

\alpha =\frac{1}{2} est surprenant au premier abord; mais pas tant que ça finalement


>> Kévin C' est parce que je savais que ça allait être "joli" que je me suis lancé dans ce topic

Posté par
ianlunare : Courbes Paramétrées du plan 25-05-10 à 12:57

Bonjour ,

cailloux comment arrive à cette conclusion à la question 3 ?
berry peut tu nous donner la suite ?

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 25-05-10 à 13:29

C'est juste un passage en coordonnées polaires:

Avec \theta_t=(\vec{\omega_tM_t},\vec{\omega_t C_t})=\frac{t}{\alpha}\;\;[2\pi], on a:

\phi_t=(\vec{i},\vec{\omega_tM_t})=t-\theta_t=\frac{\alpha -1}{\alpha}t\;\;[2\pi]

et \vec{\omega_tM_t}=r\,\cos\,\phi_t\vec{i}+r\,\sin\,\phi_t\vec{j}

\vec{\omega_tM_t}=\alpha R\,\cos\,\left(\frac{1-\alpha}{\alpha}t\right)\,\vec{i}-\alpha R\,\sin\,\left(\frac{1-\alpha}{\alpha}t\right)\,\vec{j}

Puis le résultat final avec \vec{OM_t}=\vec{O\omega_t}+\vec{\omega_tM_t}

\{X_{M_t}=R\left[(1-\alpha)\,\cos\,t+\alpha\,\cos\,\left(\frac{1-\alpha}{\alpha}t\right)\right]\\Y_{M_t}=R\left[(1-\alpha)\,\sin\,t-\alpha\,\sin\,\left(\frac{1-\alpha}{\alpha}t\right)\right]

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 25-05-10 à 13:31

Euh... Bonjour au fait!

Posté par
ianlunare : Courbes Paramétrées du plan 25-05-10 à 20:17

Bonjour et merci !

j'attends maintenant la suite ...

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 25-05-10 à 20:24

Bonsoir,

En attendant, pour tout savoir sur les hypocycloïdes (mais pas seulement), tu peux regarder l' excellent site Mathcurve:

Posté par
Berryre : Courbes Paramétrées du plan 26-05-10 à 11:05

Bonjour et excuser moi du retard

Voici la suite :

On suppose =1/3

a) - Comparer f1/3(-t) à f1/3(t)
   - Comparer f1/3(t + 2/3) à f1/3(t). Pour y parvenir, utiliser la notation complexe, c'est à dire : le point M(t) de la courbe a pour affixe z(t)=x(t) + iy(t) et donc il suffit de comparer z(t) à z(t + 2/3).
   - Interpréter géométriquement vos résultats. Sur quel intervalle I suffit-il d'étudier la trajectoire H(1/3) ?

b) Déterminer le vecteur dérivé f'1/3(t). En déduire les instants t I correspondant aux point M(t) stationnaires de H(1/3).

c) Etudier les variations de x et y sur I.

d) Préciser la nature et les tangentes aux points de paramètres 0 et /3. Démontrer que la tangente en M(/3) est orthogonale au vecteur OM(/3).

e) Construire la trajectoire H(1/3) de M(t) lorsque t parcourt .

Voilà.

Merci cailloux pour le lien, je ne savais pas que les maths c'étaient aussi jolis

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 26-05-10 à 11:57

Re,

Tu as pu faire la suite ?

Posté par
Berryre : Courbes Paramétrées du plan 26-05-10 à 12:28

A vrai dire pas vraiment.
Je ne sais pas trop quelles conclusions tirées pour chaque question.

Par exemple, j'ai trouvé que c'était symétrique par rapport à Ox et Oy.
J'ai pas trop compris à quoi ça servait de passer en mode complexe ...
Mais je cherche encore

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 26-05-10 à 14:11

a) Pour \alpha =\frac{1}{3}:

\{x(t)=\frac{R}{3}\left(2\,\cos\,t+\cos\,2t\right)\\y(t)=\frac{R}{3}\left(2\,\sin\,t-\sin\,2t\right)

Ces fonctions de t sont périodiques de période 2\pi donc à priori une étude sur [0,2\pi]

On a \{x(-t)=x(t)\\y(-t)=-y(t)

Donc si M(x,y)\in H, alors M'(x,-y)\in H

La coube présente donc une symétrie par rapport à l' axe des abscisses (mais pas l' axe des ordonnées comme tu l' as écrit).

En passant aux complexes:

z(t)=x(t)+iy(t)=\frac{R}{3}\left[2e^{it}+e^{-2it}\right]

et z\left(t+\frac{2\pi}{3}\right)=\frac{R}{3}\left[2e^{i\left(t+\frac{2\pi}{3}\right)}+e^{-2i\left(t+\frac{2\pi}{3}\right)}\right]

en remarquant que e^{-\frac{4i\pi}{3}}=e^{\frac{2i\pi}{3}}:

z\left(t+\frac{2\pi}{3}\right)= e^{\frac{2i\pi}{3}}\left[2e^{it}+e^{-2it}\right]

z\left(t+\frac{2\pi}{3}\right)=e^{\frac{2i\pi}{3}}\,z(t)

Autrement dit M\left(t+\frac{2\pi}{3}\right) est l' image de M(t) dans la rotation de centre O et d' angle \frac{2\pi}{3}

On étudie donc la courbe sur l' intervalle [0,\frac{2\pi}{3}] que l' on complétera par des rotations de centre O et d' angles \frac{2\pi}{3} et \frac{4\pi}{3}

4)b)c) x'(t)=-\frac{2R}{3}\left[\sin\,t+\sin\,2t\right]=-\frac{4R}{3}\,\cos\,\frac{t}{2}\,\sin\,\frac{3t}{2}\leq 0 sur [0,\frac{2\pi}{3}] et x est décroissante sur cet intervalle (de R à -\frac{R}{2}).

y'(t)=\frac{2R}{3}\left[\cos\,t-\cos\,2t\right]=\frac{4R}{3}\,\sin\,\frac{t}{2}\,\sin\,\frac{3t}{2}\geq 0 sur [0,\frac{2\pi}{3}] et y est croissante sur cet intervalle (de 0 à \frac{R\sqrt{3}}{2}).

Les points stationnaires (où le vecteur dérivé est le vecteur nul) correspondent aux points singuliers de H

Ils correspondent aussi aux points où M(t) est situé sur le grand cercle ("vitesse" nulle).

On cherche t sur [0,\frac{2\pi}{3}] tel que \{x'(t)=0\\y'(t)=0

Soit \{\cos\,\frac{t}{2}\,\sin\,\frac{3t}{2}=0\\\sin\,\frac{t}{2}\,\sin\,\frac{3t}{2}=0

système équivalent à \sin\,\frac{3t}{2}=0 qui donne t=\frac{2k\pi}{3}

Sur [0,\frac{2\pi}{3}], on obtient donc t=0 ou t=\frac{2\pi}{3}

d) En t=0, on a un point singulier.

On peut vérifier que \vec{f''(0)}=-2R\vec{i}\not=\vec{0}

et \vec{f'''(0)}=2R\vec{j} donc que la famille \left(\vec{f''(0)},\vec{f'''(0)}\right) est libre.

Le point M(0) (qui est le point A) est donc un point de rebroussement de première espèce.

La tangente à H en ce point est dirigée par \vec{f''(0)}=-2R\vec{i}

Pour t=\frac{\pi}{3}, on a le coefficient directeur de la tangente: \frac{y'}{x'}=-\frac{\sqrt{3}}{3}

et (OM_{\frac{\pi}{3}}) a pour coefficient directeur \frac{y}{x}=\sqrt{3}

Le produit des coefficients directeurs vaut -1:

Les deux droites sont donc perpendiculaires.

e) Cette astroïde mérite un petit dessin:

Courbes Paramétrées du plan


Posté par
Camélia Correcteurre : Courbes Paramétrées du plan 26-05-10 à 15:00

Bonjour cailloux C'est là qu'un truc qui bouge serait utile...

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 26-05-10 à 15:07

Bonjour Camélia,

Mais oui! j' y ai bien pensé dans ce topic.

Mais aussi dans certains topics de descriptive avec des intersections cônes/cylindres par exemple.

Peut-être un jour...

Posté par
infophilere : Courbes Paramétrées du plan 26-05-10 à 18:08

C'est vrai c'est dommage que geogebra ne propose pas une exportation en .gif comme le fait Maple par exemple.

Une alternative serait d'utiliser un logiciel tel que Cam Studio qui permet de filmer son écran et de créer un gif animé à partir de images capturées.

Posté par
cailloux Correcteurre : Courbes Paramétrées du plan 26-05-10 à 21:46

>>Kévin Je n' y connais rien dans ces logiciels mais il est possible qu' un jour la chose soit possible sur l'

J' en profite pour rectifier une erreur: j' ai parlé plus haut d' astroïde (qui correspond à \alpha=\frac{1}{4}) avec 4 arches) ; il s' agit en fait ici d' un deltoïde.

Posté par
Berryre : Courbes Paramétrées du plan 27-05-10 à 00:20

Merci à tous pour l'aide, et en particuler à cailloux


Rechercher
Menu
Espace membre
30 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1729 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !