Niveau Maths sup

Courbes paramétrées, Epicycloïdes et Hypocycloïdes

Posté par
sebmusik 15-11-06 à 18:35

Bonjour,
Je fais appel à vous mathîliens car je suis bloqué sur mon devoir de mathématiques, j'aimerais donc fortement que vous m'aidiez merci.

Le plan P est rapporté à un repere orthonormal direct $R$ =(O,i,j), R et r designent deux reels strictement positifs.
Soit le cercle de centre O et de rayon R et A le point d'affixe R.
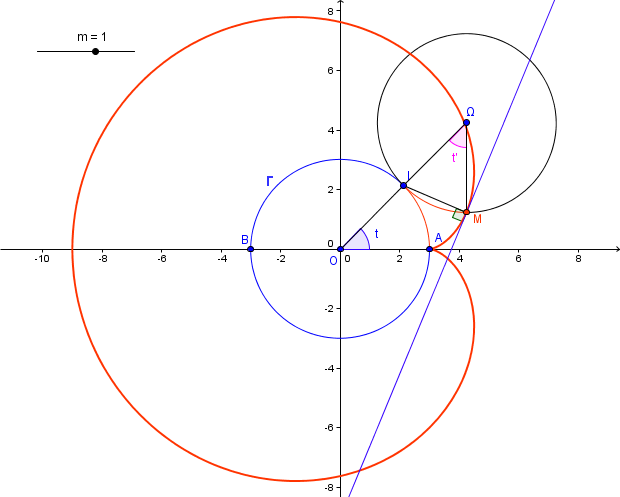
On se propose d'étudier la trajectoire d'un point mobile M lié a un cercle-mobile C de rayon r qui roule sans glisser sur le cercle fixe .
Soit I le point de contact entre le cercle fixe et le cercle roulant C, on choisit comme parametre un reel t qui soit une mesure en radians de l'angle orienté $(\vec{OA},\vec{OI})$ .
On suppose qu'a la date t=0, la position du point-mobile M a pour affixe R.

Equations

1) Determiner l'affixe du point centre du cercle C de rayon r exterieurement tangent à au point I.

2) Soit t' une mesure en radians de l'angle orienté $(\vec{\Omega I},\vec{\Omega M})$ . On suppose que t et t' verifient les deux conditions: $0\le t\le 2\pi$ et $0\le t'\le 2\pi$ . Determiner une relation simple entre t et t' qui traduit le fait que le cercle C roule sans glisser sur le cercle .

3) La relation precedente determine t' en fonction de t, on etend cette relation a un reel quelconque t, elle determine alors la position du point-mobile M a une date t quelconque. On considere la courbe paramétrée definie par la fonction $F :\mathbb{R}->P$ qui a tout reel t associe le point M. Calculer en fonction de t, R et r l'affixe z du point M.(formule 1)

4) On reprend les questions 1), 2), 3) en supposant cette fois-ci que le cercle C est interieurement tangent à (On pourra distinguer deux cas de figure suivant que r est inferieur ou superieur à R). Calculer en fonction de t, R et r l'affixe z du point M.(formule 2)

5) Montrer que les formules 1 et 2 peuvent s'ecrire chacune sous la forme suivante:
$z=Re^{it}(1+m-me^{it/m})$ . On precisera m en fonction de r et R suivant les deux cas.

Construction

Dans cette partie, m designe un nombre reel fixé non nul. On etudie la courbe parametree $(C_m,F_m)$ où $F_m$ est la fonction qui a tout reel t associe le point M d'affixe $Re^{it}(1+m-me^{it/m})$ relative au repere $R$ .

6) Montrer que, suivant les valeurs du reel m, la trajectoire $C_m$ de la courbe parametree est ou bien entierement incluse dans le disque limité par ou bien entierement a l'exterieur de ce meme disque, on precisera suivant les valeurs de m.

7) Demontrer que l'ensemble de la trajectoire de $C_m$ se deduit geometriquement de l'arc de la courbe parametree correspondant à l'intervalle $[0,\pi|m|]$ .

8) Demontrer que le vecteur $\vec{IM}$ est orthogonal à la tangente à la trajectoire au point M.

9) Demontrer que, pour tout reel m verifiant m0 et m-1, les courbes $C_m$ et $C_{-1-m}$ sont egales.

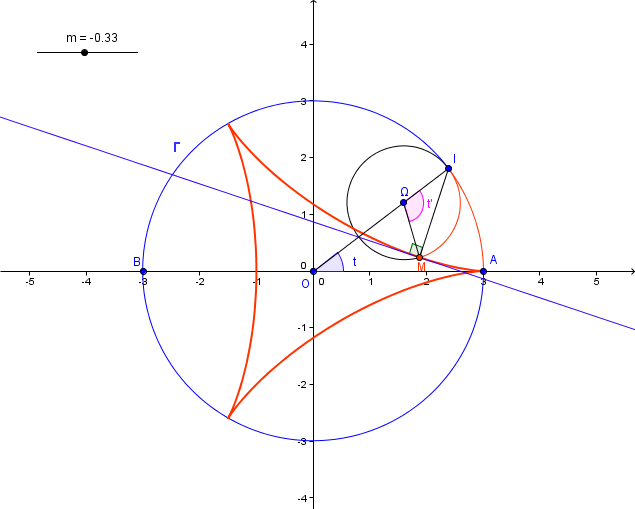
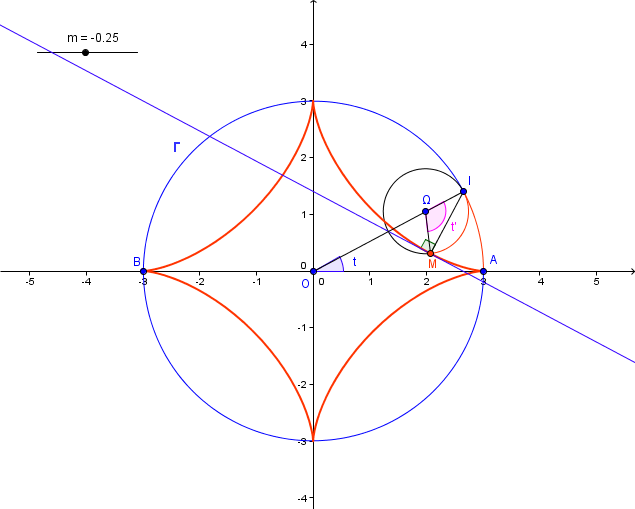
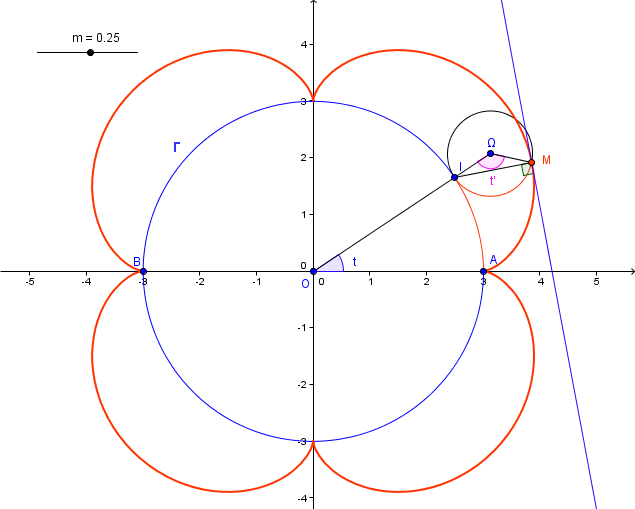
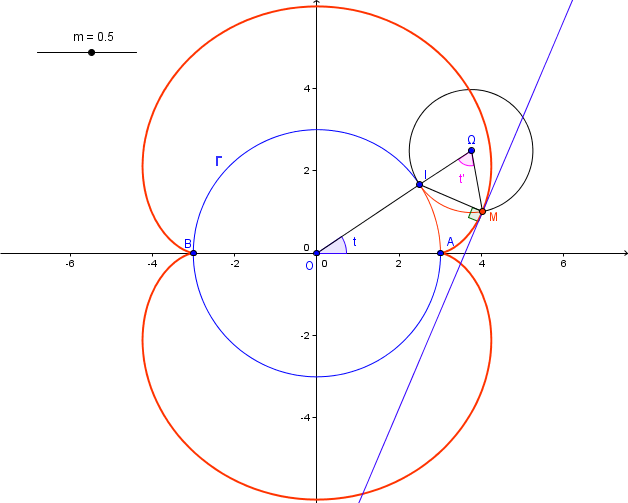
10) Dessiner les courbes pour les valeurs suivantes de m : -1/2 , -1/3 , -1/4 , 1/4 , 1/2 , 1

Mes resultats

1) $O\Omega=R+r$ donc a pour affixe $((R+r)cost + i(R+r)sint)$ soit $[R+r)e^{it}$

2) longueur arc(AI)=Rt et longueur arc(IM)=rt' or longueur arc(AI)= longueur arc(IM) puisque le cercle C roule sur le cercle fixe donc Rt=rt' ou encore t'=Rt/r

3) t'=Rt/r, t un reel quelconque
M(z) mais comment trouver z en fonction de t,R et r?

Seb

Posté par re : Courbes paramétrées, Epicycloïdes et Hypocycloïdes 10-08-10 à 11:25

Un vieux topic...

1)
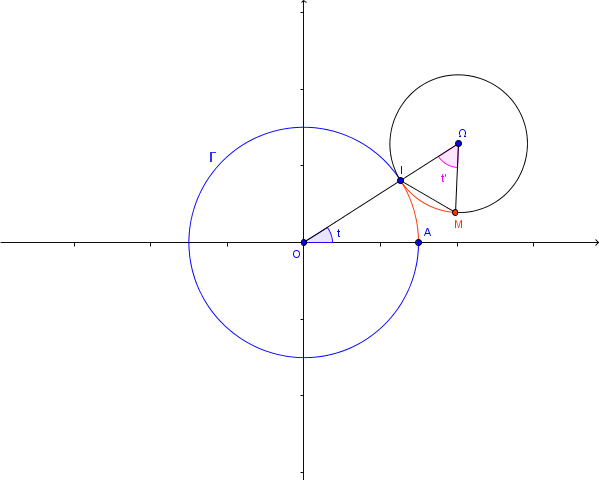
Courbes paramétrées, Epicycloïdes et Hypocycloïdes

$\fbox{z_{\Omega}=(R+r)e^{it}}$

2) $\stackrel{\frown}{IM}=\stackrel{\frown}{AI}$

$rt'=Rt$ d' où $\fbox{t'=\frac{R}{r}t}$

3) $\vec{OM}=\vec{O\Omega}+\vec{\Omega M}$ avec $z_{\vec{\Omega M}}=re^{i(\vec{OA},\vec{\Omega M})}$

$(\vec{OA},\vec{\Omega M})=(\vec{OA},\vec{OI})+(\vec{OI},\vec{\Omega M})=(\vec{OA},\vec{OI})+(\vec{\Omega I},\vec{\Omega M})+\pi\;\;[2\pi]$

$(\vec{OA},\vec{\Omega M})=t+t'+\pi=\left(1+\frac{R}{r}\right)t+\pi\;\;[2\pi]$

d' où, avec $z(t)$ l' affixe de $M$ :

$\fbox{z(t)=(R+r)e^{it}-re^{i\left(1+\frac{R}{r}\right)t}}$ (1)

4) Un nouveau cas de figure avec $C$ tangent intérieurement à $\Gamma$ et $r<R$ :

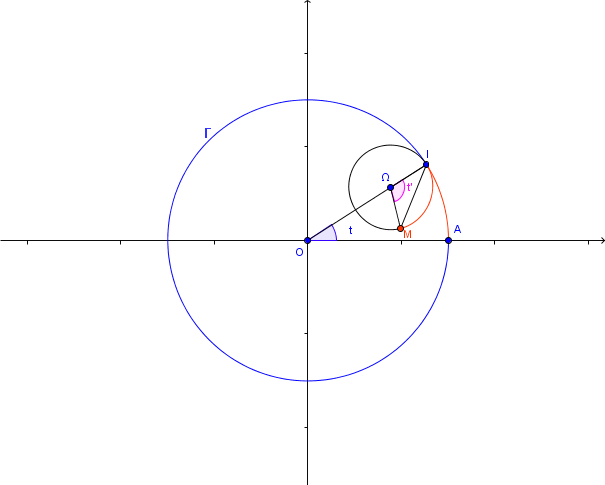
Courbes paramétrées, Epicycloïdes et Hypocycloïdes

On a maintenant: $\fbox{z_{\Omega}=(R-r)e^{it}}$

$\stackrel{\frown}{IM}=-\stackrel{\frown}{AI}$

$rt'=-Rt$ d' où $\fbox{t'=-\frac{R}{r}t}$

et $(\vec{OA},\vec{\Omega M})=(\vec{OA},\vec{OI})+(\vec{OI},\vec{\Omega M})\;\;[2\pi]$

$(\vec{OA},\vec{\Omega M})=t+t'=\left(1-\frac{R}{r}\right)t\;\;[2\pi]$

et $z(t)=(R-r)e^{it}+re^{i\left(1-\frac{R}{r}\right)t}$

Un nouveau cas de figure avec $C$ tangent intérieurement à $\Gamma$ et $r>R$ :

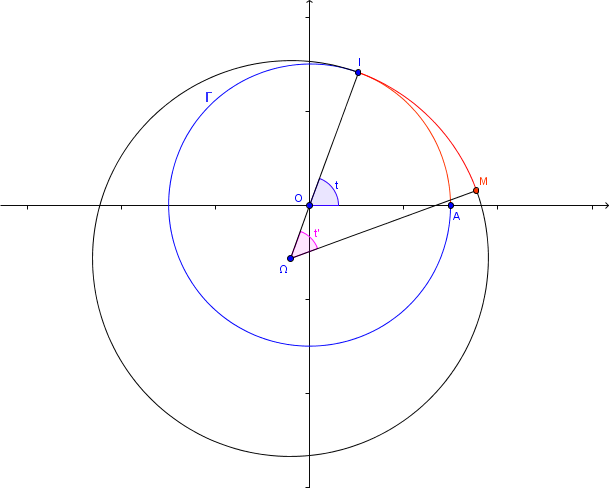
Courbes paramétrées, Epicycloïdes et Hypocycloïdes

On a maintenant $z_{\Omega}=(r-R)e^{i(t+\pi)}$

soit: $\fbox{z_{\Omega} =(R-r)e^{it}}$

$\stackrel{\frown}{IM}=-\stackrel{\frown}{AI}$

$rt'=-Rt$ d' où $\fbox{t'=-\frac{R}{r}t}$

et $(\vec{OA},\vec{\Omega M})=(\vec{OA},\vec{OI})+(\vec{OI},\vec{\Omega M})\;\;[2\pi]$

$(\vec{OA},\vec{\Omega M})=t+t'=\left(1-\frac{R}{r}\right)t\;\;[2\pi]$

et $z(t)=(R-r)e^{it}+re^{i\left(1-\frac{R}{r}\right)t}$

Donc dans le cas où le cercle $C$ est tangent intérieurement à $\Gamma$ , on a:

$\fbox{z(t)=(R-r)e^{it}+re^{i\left(1-\frac{R}{r}\right)t}}$ (2)

5) a) Cercle $C$ tangent extérieurement à $\Gamma$ :

$z(t)=Re^{it}\left(1+\frac{r}{R}-\frac{r}{R}e^{i\frac{Rt}{r}}\right)$

En posant $m=\frac{r}{R}$ , on obtient:

$z(t)=Re^{it}\left(1+m-me^{i\frac{t}{m}}\right)$

b) Cercle $C$ tangent intérieurement à $\Gamma$ :

$z(t)=Re^{it}\left(1-\frac{r}{R}+\frac{r}{R}e^{-i\frac{Rt}{r}}\right)$

et en posant $m=-\frac{r}{R}$ , on obtient:

$z(t)=Re^{it}\left(1+m-me^{i\frac{t}{m}}\right)$

Donc avec la convention $m>0$ si $C$ est tangent extérieurement à $\Gamma$ et $m<0$ si $C$ est tangent intérieurement à $\Gamma$ , on obtient en posant $|m|=\frac{r}{R}$ :

$\fbox{z(t)=Re^{it}\left(1+m-me^{i\frac{t}{m}}\right)}$

6) Supposons $m>0$ (cercle $C$ tangent extérieurement à $\Gamma$ )

$\left|1+m-me^{i\frac{t}{m}}\right|\geq |1+m|-|m|$

$\left|1+m-me^{i\frac{t}{m}}\right|\geq 1+m-m$

$\left|1+m-me^{i\frac{t}{m}}\right|\geq 1$

donc $\fbox {|z(t)|\geq R}$ et $M$ est toujours à l' extérieur de $\Gamma$

Supposons $m<0$ (cercle $C$ tangent intérieurement à $\Gamma$ )

$\left|1+m-me^{i\frac{t}{m}}\right|\leq |1+m|+|-m|$

$\left|1+m-me^{i\frac{t}{m}}\right|\leq |1+m|-m$

- Si $m\leq -1$ , on a $\left|1+m-me^{i\frac{t}{m}}\right|\leq -2m-1\leq 1$

- Si $-1\leq m <0$ , on a: $\left|1+m-me^{i\frac{t}{m}}\right|\leq m+1-m$ soit $\left|1+m-me^{i\frac{t}{m}}\right|\leq 1$

donc $\fbox {|z(t)|\leq R}$ et $M$ est toujours à l' intérieur de $\Gamma$

7) $z(t+2|m|\pi)=Re^{i(t+2|m|\pi)}\left(1+m-me^{i\frac{t+2|m|\pi}{m}}\right)$

$z(t+2|m|\pi)=e^{2i|m|\pi}Re^{it}\left(1+m-me^{i\frac{t}{m}}\right)$

$\fbox{z(t+2|m|\pi)=e^{2i|m|\pi}z(t)}$

Ainsi, $M(t+2|m|\pi)$ est l' image de $M(t)$ dans la rotation $r$ de centre $O$ et d' angle $2|m|\pi$

On se limite donc à une étude sur $[0,2|m|\pi]$ suivie de rotations $r$ .

$\left|z(t+|m|\pi)\right|=R\left|1+m+me^{it}\right|$

$\left|z(-t+|m|\pi)\right|=R\left|1+m+me^{-it}\right|=R\left|\overline{1+m+me^{it}}\right|$

donc $\fbox{\left|z(-t+|m|\pi)\right|=\left|z(t+|m|\pi)\right|}$

et sur l' intervalle $[0,2|m|\pi]$ , la courbe présente une symétrie par rapport à la droite d' équation $\theta =|m|\pi$

D' où étude sur $[0,|m|\pi]$ suivie d' une symétrie par rapport à la droite d' équation $\theta =|m|\pi$ et de rotations $r(O,2|m|\pi)$

8) $z_{\vec{IM}}=Rme^{it}\left(1-e^{i\frac{t}{m}}\right)$

$z'(t)=R\left[ie^{it}\left(1+m-me^{i\frac{t}{m}}\right)-ie^{it}e^{i\frac{t}{m}}\right]$

$z'(t)=iR(m+1)e^{it}\left(1-e^{i\frac{t}{m}}\right)$

On a donc:

$z_{\vec{IM}}\overline{z'(t)}+\overline{z_{\vec{IM}}}z'(t)=-iR^2m(m+1)\left(1-e^{i\frac{t}{m}}\right)\left(1-e^{-i\frac{t}{m}}\right)+iR^2m(m+1)\left(1-e^{-i\frac{t}{m}}\right)\left(1-e^{i\frac{t}{m}}\right)$

$\fbox{z_{\vec{IM}}\overline{z'(t)}+\overline{z_{\vec{IM}}}z'(t)=0}$

Donc $\vec{IM}$ est orthogonal à la tangente à la trajectoire en $M$ .

9) $z_{-1-m}(t)=Re^{it}\left[1-1-m+(m+1)e^{-i\frac{t}{m+1}}\right]$

$z_{-1-m}(t)=Re^{it\left(1-\frac{1}{m+1}\right)}\left[m+1-me^{i\frac{t}{m+1}}\right]$

$z_{-1-m}(t)=Re^{i\frac{mt}{m+1}}\left(1+m-me^{i\frac{t}{m+1}}\right)$

d' où:

$\fbox{z_{-1-m}\left(\frac{m+1}{m}t\right)=z(t)}$

Donc pour $m\not=0$ et $m\not=-1$ , les courbes $C_{-1-m}$ et $C_m$ sont identiques.

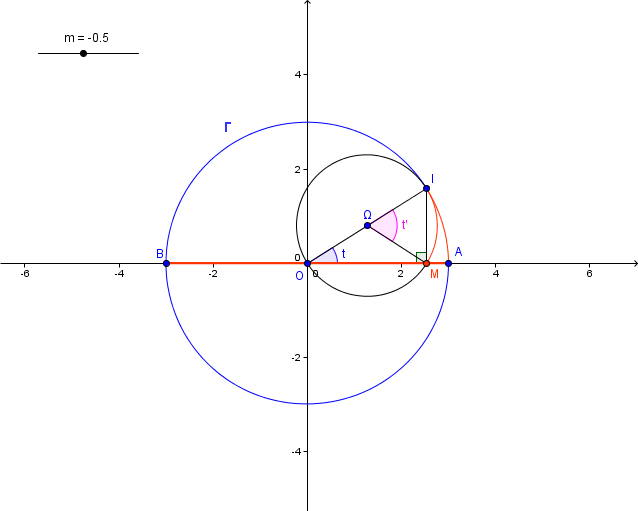
Posté par re : Courbes paramétrées, Epicycloïdes et Hypocycloïdes 10-08-10 à 11:27

10)

Courbes paramétrées, Epicycloïdes et Hypocycloïdes

Posté par re : Courbes paramétrées, Epicycloïdes et Hypocycloïdes 10-08-10 à 11:28

Courbes paramétrées, Epicycloïdes et Hypocycloïdes

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

géométrie en post-bac
4 fiches de mathématiques sur "géométrie" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

9 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Courbes paramétrées, Epicycloïdes et Hypocycloïdes

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths