J'ai trouvé une valeur approchée du côté du cube : 4,57 .

salut

pour dégrossir ... sans savoir où je vais réellement ...

le cube est inscrit dans une sphère tangente au plan en un sommet du cube

en prenant pour plan le plan (Oxy) et pour sommet du cube dans le plan l'origine O

en notant c le côté du carré alors l'équation de la sphère est

on cherche donc sept points (enfin pas besoin de tous) de la sphère à distance 1, 2, 3, 4, 5, 6 et 7 de O

peut-être simplement s'intéresser à ces questions :

quelles sont les distances entre deux sommets d'un cube ?
quelles sont les ordonnées des sommets du cube ?

...

Bonjour,

  On tombe sur après des calculs ...  pénibles

Bonjour,

est le sommet de contact du cube et du plan.

On choisit un repère en sorte que soit orthogonal au plan.

Le problème est entièrement fixé lorsque 3 sommets sont déterminés.

Si on choisit de cote , de cote et de cote avec trièdre trirectangle  en et , le 4ème point de la face aura pour cote .

Les 3 derniers sommets seront les translatés de par le vecteur de cote , ils auront pour cote

Maintenant, on peut commencer les calculs: des produits scalaires nuls et des normes qui valent

C'est pénible mais on aboutit à

J'ai oublié: pour "simplifier", on commence avec dans le plan

mathafou : ok pour la première remarque ... évidemment ... (et c'est ce que j'avais vu dans ma tête en premier d'ailleurs)

deuxième remarque : bien sur ... d'où ma deuxième question

un dessin m'aurait permis d'être plus ... efficace

Bonjour,
Je donne aussi mon "dégrossissement" ... que je peine à faire aboutir

Les sommets du cube de côté f : O, A, B, C, O',A',B',C' .

Un repère orthonormé

Un plan (P) d'équation ax+bx+c+d = 0 avec a²+b²+c² =1 et d > 0 .
Tous les sommets du cube sont du même côté du plan (P) . C'est à dire dans le même demi espace.
La distance du point O au plan (P) est d . On peut donc écrire les 7 autres distances sans valeur absolue.
Il reste à utiliser que ces 8 distances sont 0, 1, 2, ... , 7 dans le désordre.

Plein de réponses pendant que j'écrivais
Je ne vais pas avoir le temps tout de suite, mais je regarderai en fin d'après midi.

Sylvieg ta démarche est la bonne et donne des calculs "très simples"
à condition de bien partir en 3D dès le départ !!
je renomme tout ça avec un cube nommé comme d'habitude ABCDEFGH
et le repère orthonormé d'origine A et d'unité l'unité de distance, porté par les arêtes du cube issues de A

A (0; 0; 0)
B (d; 0; 0)
D (0; d; 0)
E (0; 0; d)
en appelant d l'arête du cube
un plan passant par A donc d'équation ax+by+cz = 0
pour simplifier les calculs de distance on peut imposer a²+b²+c²= 1
alors la distance de B au plan est = ad
celle de D au plan est bd
et celle de E au plan = cd

trouver sans calcul ou presque les valeurs numériques distances de B,D,E au plan
(c'est à dire trouver qui ests qui parmi {0, ...7} :
considérer que le centre de gravité du triangle équilatéral BDE découpe la grande diagonale AG au tiers
en projetant la relation obtenue sur la perpendiculaire au plan
on obtient h_B + h_D + h_E = 7
et donc parmi les nombres donnés sauf 0 et 7, il n'y a qu'une seule façon d'obtenir une somme de trois nombres = 7
donc "sans perte de généralité"
on a ad = 1, bd= 2 et cd= 4

par conséquent
1/d² + 4/d² + 16/d² = 1 et d² = 21
terminé ou presque : il reste à vérifier chacune des distances des autres sommets à ce plan là.
(rien ne prouve que les valeurs données sont cohérentes avec un vrai cube)
cela peut se faire par des calculs sur les coordonnées
ou bien en poursuivant le raisonnement qui a aboutit au trois premières distances et les obtenir toutes "sans calcul"

Merci mathafou
Je me disais bien que ça devait aboutir sans trop de calculs.
Il fallait faire passer le plan par un des sommets du cube. L'origine du repère étant à privilégier...

Le cube "posé" sur le plan permet de justifier que ad , bd et cd sont de même signe, donc positifs (après une éventuelle multiplication par -1 de l'équation du plan )

A mon avis, inutile de faire intervenir diagonales et projections.
Les distances au plan sont :
ad pour B , bd pour D , cd pour E , ad+bd pour C , ad+cd pour F , bd+cd pour H .
La distance du point G au plan est ad +bd +cd .
Les autres sont inférieures ; donc ad +bd +cd = 7 .

oui, on peut faire ça comme ça
j'étais parti dès le départ sur ces histoires de qui est qui comme distances (donc sans repère ni équation de plan du tout)
c'est pour ça que je l'ai repris ainsi tel quel
mais comme tu fais c'est directement plus rapide et donne le même résultat :
la seule façon avec les valeurs fournies d'avoir ad +bd +cd = 7 est 1, 2, 4 dans l'ordre qu'on veut

par contre je m'interroge sur le fond
équation de plan en 1ère et distance d'un point à un plan ??
sans ces connaissances là c'est beaucoup plus compliqué !!

Pour ma part, j'ai utilisé une méthode trigonométrique qui devrait être accessible à un élève de première.

Oui, moi aussi je me suis interrogée. C'est pour ça que je n'ai pas donné ma piste qui utilise ces connaissances. Surtout que je n'aboutissais pas...
Je me disais qu'il pouvait y avoir un autre cheminement niveau première.

@Priam,
Chic, une nouvelle piste

comme le cube est "tout de travers" par rapport au plan (ou le plan tout de travers par rapport au cube) les autres méthodes sont comme le dit lake "pénibles"
et déja bien plus complexes à visualiser

salut,
parfois je me demande s'il ne faudrait pas demander au posteur sa moyenne de math
histoire d'etre au niveau ...

Bonjour,

En reprenant la démarche de lake du  05-03-18 à 13:54
je trouve une solution tout à fait à portée d'un élève de première sans que les calculs soient "pénibles"...
Ce doit d'ailleurs être ce que Priam avait fait

On choisit A de cote 0, B de cote 1, C de cote 3, D de cote 2 et E de cote 4 avec a longueur de l'arête : le cube ABCDEFGH est en place sur le plan horizontal P

Si M est l'intersection de (BC) avec le plan P le triangle ABM dans le plan ABCD est rectangle en B et AB=a et BM=a/2. La hauteur issue de B est BH=a/5
l'angle dièdre des plans ABCD et P est
mais le coté [AE] fait cet angle avec sa projection sur P, alors
d'où cos²+ sin²=1 a²=21

Joli travail d'équipe
Une coquille peut-être pour BM et BH . Je trouve BM = 2a et BH = 2a/5 .

On a bien .
La "complexité", comme dit mathafou, est de visualiser !
En notant H_B le projeté orthogonal de B sur le plan, est une mesure de l'angle en H du triangle rectangle BHH_B .
C'est du moins ce que j'ai compris...

Bonjour,

--> Sylvieg : avec mes notations BC=a   B a une cote de 1, C une cote de 3, donc M avec une cote de 0 sur (BC) du côté de B est tel que BM=a/2
Puis dans le triangle ABM, si H est le pied de la hauteur issue de B alors BH=a/5.
Comme B a une cote de 1 si on le projète sur P en B_H alors l'angle BHB_H= et sin=(5)/a  .....

D'accord, j'avais mal écrit le 1 sur ma figure et lu 2

En fait, l'erreur que j'ai faite revient à calculer sin en utilisant le sommet D de cote 1 au lieu du sommet B de cote 2 .
Heureusement, on trouve le même résultat

Bonjour,
les cotes "choisies" doivent être justifiées (voir dans la discussion au dessus)
et faire un dessin un tant soit peu réaliste de ce plan en biais et de sa perpendiculaire en A (AE) et des projections de tout ça sur (P) n'est pas une mince affaire ...
on peut faire faire ça par Geogebra 3D
mais ce n'est pas non plus une mince affaire
surtout avec le graphisme extrêmement moche de Geogebra 3D et la difficulté (euphémisme) de maitriser tout ce qu'on veut comme on veut, et pas comme ça chante au logiciel.



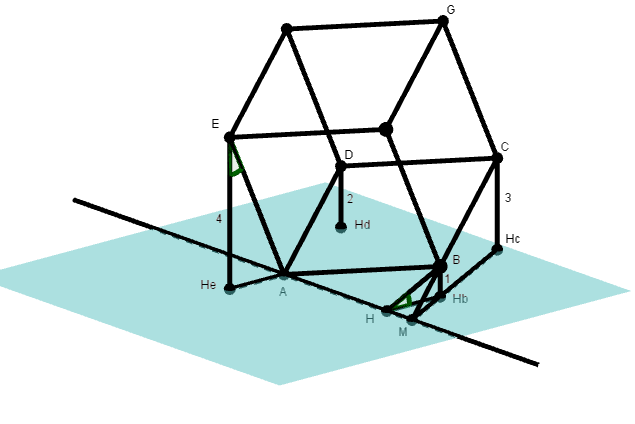
(figure de principe pas à l'échelle, juste le cube est un vrai cube et les angles droits de vrais angles droits etc)

Bonjour mathafou,
Bravo pour la figure
Les cotes ont été justifiées par lake (message du 05-03-18 à 13:54).

pas vraiment.

il dit dans son message "Si on choisit ..."
sans dire pourquoi.
les seules justifications véritables données ici sont :
via l'équation du plan etc (ta méthode et mon additif sur la seule façon d'avoir une somme = etc, ou sur le tri de ces valeurs)
via les projections des relations vectorielles dans le cube (ma méthode) et toujours "la seule façon d'avoir une somme = etc
ou le tri de ces projections par ordre croissant

une justification que les 4 valeurs du trièdre ABDE sont les 4 plus petites de la liste et basta nécessite une vision parfaitement claire dans l'espace de la position d'un cube par rapport à un plan, pour pouvoir dire que ce serait "intuitivement évident"
mais cela ne serait formalisé que par les projections de sommes de vecteurs sur la verticale au plan , comme j'ai dit, finalement.

Je détaille, avec les points de la figure :
z_A = 0 z_C = z_B+z_D
z_F = z_B+z_E z_H = z_D+z_E z_G = z_B+z_D+z_E

D'où z_G = 7 et les seules cotes possibles 1,2,4 pour B, D, E dans le désordre.

nota : Z_C = Z_B+Z_D est la traduction de la projection sur un axe vertical de la relation vectorielle :



ou la traduction de cette somme sur l'axe des cotes (les composantes z de ces vecteurs)

ou du fait que le milieu de AC est le milieu de BD : Z_C/2 = (Z_B+Z_D)/2

etc
il y a plusieurs façons de voir et de dire la même chose...
l'essentiel est de le dire

copier coller malheureux mal relu

Oui
En fait, l'objectif au départ n'était pas de donner une solution toute mâchée, mais d'indiquer des pistes à Bezere.
Il a d'ailleurs brillé par son absence de réaction

Avec des milieux, me viens encore une autre manière "de voir et de dire la même chose"
pour démontrer z_G = 7 :
Le centre du cube est le milieu de ses 4 diagonales.
D'où z_A+z_G = z_B+z_H = z_C+z_E = z_D+z_F .
Or la somme des 8 cotes est 28 . D'où z_A+z_G = z_B+z_H = z_C+z_E = z_D+z_F = 7 .


PS Peux-tu aller voir Puissances de 76 ?
Vers la fin, une formule de ton site y est utilisée. En connais-tu la provenance ?