Inscription / Connexion Nouveau Sujet
cylindre dans un cone
Bonjour j'ai un ex de maths a faire:
Le cone a pour hauteur 10cm et pour rayon 6cm, et le cylindre inscrit à l'intérieur a pour hauteur h et pour rayon r
1) Montrer que le volume du cylindre s'exprime en fonction de r par V(r)=pi * r^2( 10 -(5/3)r).
2) On note f la fonction définie sur 0;6 par f(x)=pi * x^2( 10 -(5/3)x).
a) Montrer que f'(x) est du même signe que x(4-x).
b) Puis dresser le tableau de variation de la fonction f.
3) En déduire la valeur de r pour laquelle le volume du cylindre inscrit dans le cone est maximale, et donne cette valeur maximale.
4) Finalement, le parfumeur souhaite que la contenance du cylindre soit égale à 125mL. Combien de possibilité aura-t-il ?
Pour chacune d'entre elles, on donnera un encadrement du rayon r au centième près.
Bonjour,
il est obligatoire que tu dises ce que tu as commencé, essayé, fait et exactement ce qui t'empêche d'avancer
"rien du tout" n'est ni crédible ni accepté.
commencer par un dessin s'il n'y en pas déja un
pour joindre une figure (que uniquement des figures) lire la FAQ ![]() [lien]
[lien]
oups j'ai oublié. J'étais parti sur autre chose.
Pour la 1), je sais qu'il faut mettre la formule du volume d'un cylindre qui est de pi*r^2*h
je suis censé mettre que h=10-(5/3)r
Pour la 2)b), je suis censé faire le tableau de signe f'(x) puis mettre les variation de f(x); c'est pour la 2)a) que je ne comprends pas ce que je doit faire. Pour la 3), il suffit que je calcule la valeur max obtenue en faisant le delta de f'(x). Cette valeur je l'utilise dans f(x)
Mais pour la 4) je crois qu'il faut que je mette que : pi * x^2( 10 -(5/3)x)=125
donc pi * x^2( 10 -(5/3)x)-125=0 et que je refasse delta
la formule du volume d'un cylindre est pi*r^2*h. La formule que l'on doit donner est V(r)=pi * r^2( 10 -(5/3)r) donc j'en ai déduit que h=10-(5/3)r
tu confonds démontrer quelque chose et deviner ce qu'il faudrait démontrer en partant du résultat attendu (ils sont bien bons de le donner ce résultat attendu !!)
la question 1 c'est à partir de la figure dans laquelle on va voir une application du théorème de Thalès.
et une fois le volume calculé sans à priori en fonction de r, seulement là tu pourras vérifier que tes calculs sont justes en comparant à ce qui est donné comme formule.
la 2a c'est déja commencer par dériver !!
une fois cette dérivée obtenue, tu verras bien ce qu'il faut en faire pour arriver à ce qui est demandé (son signe)
faire déja ça avant d'anticiper avec des plans sur la comète ...
(la 3 c'est utiliser les résultats de la 2 etc donc sans ces résultats c'ets du pur baratin)
mais je ne comprends pas bien ce que je dois faire pour la question 1: le théorème de thales puis calculer le volume ? Et pour les autres question je vois a peut près ce que je dois faire
En TS ,on ne fait pas d'à peu pres ...ailleurs non plus!
Tu as deux inconnues h et r , donc visiblement d'apres la formule demandée que dois tu chercher à faire?
et oui j'ai fait un dessin
montre le,
parce que si ça se trouve il ne montre rien du tout ton dessin :
noms de points pour pouvoir appliquer Thalès (déja dit)
appliquer Thalès ne veut pas dire "je dois appliquer Thalès" et ne rien en faire du tout (que du baratin) mais l'appliquer explicitement
donc écrire les égalités.
ça c'est encore du baratin
bien sûr le volume fonction de r,
mais ça ne viendra pas tout seul comme ça :
écrire les égalités de Thalès à partir de ton dessin
ça donnera h en fonction de r et donc au final une formule avec que du r dedans
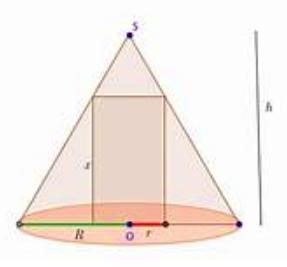
je n'arrive pas a envoyer la photo mais j'ai fais un triangle de hauteur 10cm et de base 6cm avec a l'intérieur un rectangle de hauteur h et de rayon r:
sur ce schémas ce serait b=10cm, R=3cm , x serait le h
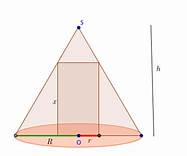
je n'arrive pas à lire tes noms de points
(indispensables pour pouvoir écrire Thalès)
c'est bien ce que je disais, cette figure est inutilisable sans la hauteur du cône tracée explicitement (c'est pas à l'extérieur !!) ainsi que les points qui sont dessus (y a pas que O et S !)
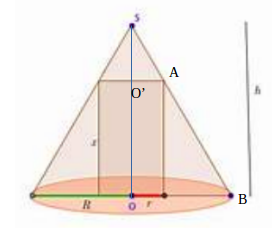
oui, on attendait un tel schéma de la part de LilyLouna
(après tout c'est à elle de choisir les noms des points)
elle peut dire merci malou !!
y a plus qu'à écrire Thalès avec ces noms de points
on peut choisir soit de "sommet" S et parallèle = O'A,
soit de "sommet" B et parallèle pas encore nommée pour écrire Thalès
un des deux donne un calcul bien plus simple que l'autre vu qu'on cherche h en fonction de r et pas r en fonction de h