Inscription / Connexion Nouveau Sujet
Démonstration par récurrence
Bonjour,
Je travaille actuellement sur la démonstration par récurrence, et j'aurai besoin de vos lumières.
Sur internet, je trouve ce site : ** lien vers l'énoncé effacé **
Je m'interesse au premier exemple (suite de nombres entiers).
Je comprends l'étape d'initialisation, mais pas vraiment l'hérédité.
On admet que la proposition est vraie pour 1+2+...+n.
On doit donc vérifier si elle est vraie pour n+1. Cependant, j'aurai eu tendance a écrire : 1+2+...+n+1 en remplacant donc le n de la proposition initiale par n+1. Seulement je remarque que c'est 1+2+...+n+(n+1).
J'aimerai que vous m'expliquiez si possible, pourquoi on ajoute (n+1) tout (en conservant le n) au lieu de remplacer n dans la proposition initiale par (n+1).
J'espere avoir été compréhensible.
Merci
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
[lien]
Le lien vers l'énoncé a été effacé, je le récris a la "main" :
1+2+...+n = 1/2n (n+1)
>Pour n=1
*C'est vrai : 1=1/2x1(1+1)
>Supposons la formule vraie pour n
*L'est elle pour n+1 ?
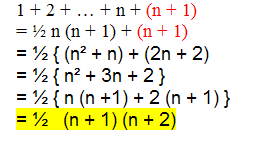
Ce qui m'interesse est pourquoi a t-on 1+2+...+n+(n+1) et non 1+2+...+n+1 comme j'aurai pensé.
Merci
Edit Coll : image placée sur le serveur de l' 
Merci d'en faire autant la prochaine fois ! [lien]
Ce qui m'interesse est pourquoi a t-on 1+2+...+n+(n+1) et non 1+2+...+n+1 comme j'aurai pensé.
1+2+...+n+(n+1) = 1+2+3+...+n+(n+1)
1+2+...+(n+1) = 1+2+3+...+n+(n+1)
c'est la même chose.
...
Bonsoir marc 
imaginons que n = 9
Donc n + 1 = 10
Donc la somme de 1 à 10 est = 1+2+...+n+(n+1) = 1+2+..+(n+1)
bonjour
somme des n premiers nombres : n(n+1)/2
en ajoutant n+1 : n(n+1)/2 + (n+1)
= (n+1) * (n/2 + 1)
= (n+1) * (n/2 + 2/2)
= (n+1) * (n+2) /2
= (n+1)*[(n+1)+1)]/2
la FAQ du forum
Annuler
connectez vous