Inscription / Connexion Nouveau Sujet
Démonstrations d'ensemble de points
Bonjour, j'espère que vous allez pouvoir m'aider malgré que ce soit assez compliqué pour moi car je suis en Licence pluri et le programme mathématiques me semble ne pas être de notre niveau.
A partir de rappel conique, d'équations d'ellipse, de parabole, d'hyperbole, de spirale etc...
On nous demande à partir d'une formule de démontrer l'ensemble des points.
Nous avons comme outil le logiciel Cabri qui nous a permit de représenter l'ens des points graphiquement. Et grâce à ce logiciel, on peut voir quel ens on doit démontré.
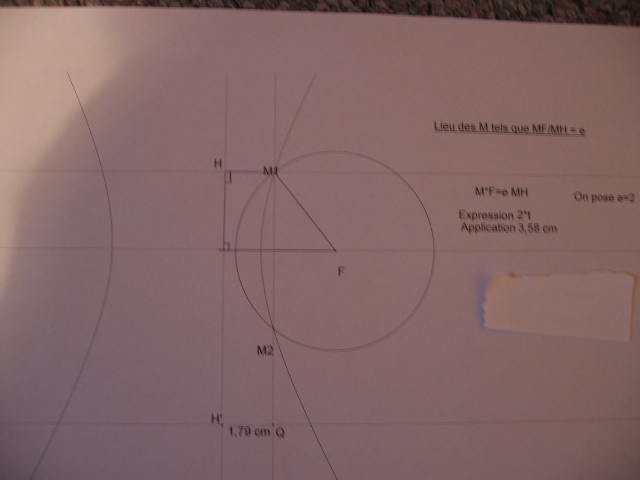
Par ex j'ai pour formule M, MF/MH=e avec e Supérieur à 1, je trace l'ens des point avec Cabri, j'obtiens une hyperbole, et c'est à moi de retrouver l'équation d'une hyperbole en partant de MF/MH=e.
Les questions sont :
1) Ens des points ou lieu géométrique de M tel que MF1+MF2=2a (a fixé, a sup à 0)(on obtient par Cabri une ellipse)
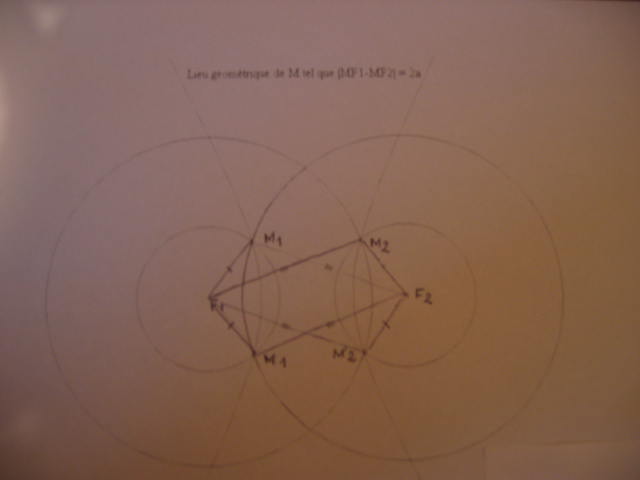
2) Ens des points de M tel que MF1-MF2 (en valeur absolue)=2a (voir figure n°2)
3) Ens des points de M tel que MF1*MF2=2a (on obtient par Cabri une ellipse mais ressérée au milieu comme une "Hémathie")
4) Ens des points de M tel que MF1/MF2=2a ( on obtient un cercle par Cabri)
5) Ens des points de M tel que MF/MH=e (e sup à 0 fixé)(voir figure n°3)
Si e inf à 1, on a une ellipse
Si e sup à 1, on a une hyperbole
Si e=1, on a une hyperbole
Je vous envoie les figures obtenues avec Cabri et une démo que j'ai commencé si cela peut vous aider.
Début de Démo (voir figure n°1)
Suite de ma démo
Donc MF1-MF2=2a
Racine de ((x+C)^2 +y^2) - Rracine de ((x+ou-C)^2+y^2)=2a
On a une équation de conique
Une fois qu'on a l'équation de conique, on la travaille pour définir si on a affaire à une ellipse ou une parabole ou une hyperbole.
Une équation conique peut s'écrire sous la forme d'une équation du 2nd degré :
x^2+y^2+xy+x+y+1=0
y^2+y(x+1)+(x^2+x+1)=0
ay^2+by+c=0
Racines de la forme xm = (+ou-) racine de (ax^2+bxm)
Equation du 2nd degré ss la racine dc doit être sup à 0
Puis étude de fonction
si a inf à 0
signe de f est du signe de -a entre les racines du signe de a à l'ext des racines donc domaine de définition borné donc ellipse
Et si a sup à 0
signe de f est du digne de -a entre les racine et du signe de a à l'ext des racines donc parabole ou hyperbole



 géométrie en post-bac
géométrie en post-bac