- Angles : angles adjacents, opposés, angles complémentaires, alternes, correspondantes... - Cours de cinquième
- Exercices sur les angles - cinquième
- Exercices sur les nombres en écriture fractionnaire - cinquième
- Dix problèmes pour revoir les acquis de la sixième - cinquième
- Quatorze Exercices pour démarrer le calcul numérique - cinquième
- Seize Exercices portant sur le programme de cinquième
- Vocabulaire cinquieme
Inscription / Connexion Nouveau Sujet
Démontrer qu'une bissectrice est parallèle à une droite
Bonjour,
j'ai un exercice :
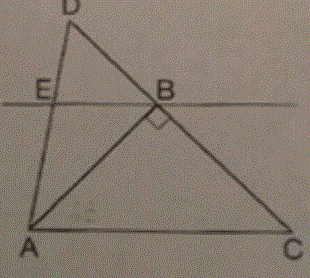
Les droites (AB) et (BC) sont perpendiculaires.
La demi droite [BE) est la bissectrices de l'angle (ABD).
Les droites (BE) et (AC) sont-elles parallèles?
Ne sachant pas comment vous faire parvenir la figure j'essai de vous l'expliquer.
Nous avons le triangle DCA, dans ce triangle un autre triangle est formé : ABC qui est rectangle en B (B appartient à la droite DC)
la demi droite [BE) forme la bissectrice de l'angle (ABD).
La définition de la bissectrice je la connais mais je ne vois pas quelle propriété utilisé pour montrer que celle-ci est parallèle à AC.
Si vous arrivez à m'aider avec cet énoncé peu clair, je vous en remercie.
Salut
tu peux facilement calculer l'angle ABE
Et en utilisant la propriété des angles alterne internes égaux
SI [BE]//[AC], alors on remarque égalité entre les angles ABE et ?
Bonjour
sans indications supplémentaires comme des codages ou des mesures (conduisant à la valeur de l'angle ACD par exemple)
c'est impossible
la figure n'est pas assez définie sans ambiguïté pour qu'une conclusion générale puise être obtenue
ce sera vrai ou pas, ça dépend de la forme du triangle ACD de départ.
Bonsoir ,
Je joins une figure qui permettra peut-être d'y voir plus clair , si elle correspond effectivement à ton exercice
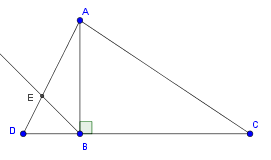
En effet (BE)//(AC) si et seulement si ABE = BAC
Or BAC dépend entièrement de DCA qu'on ne connaît pas
La figure correspond à celle que j'ai, mais dans mon énoncé je n'ai aucune mesure d'angle sauf l'angle droit formé par la perpendiculaire
donc la réponse est "on ne peut rien prouver du tout" point final
(mais ça c'est vrai si tu n'as réellement QUE ça dans ta figure et dans ton énoncé, on attend la vraie image de ta vraie figure ...)
c'est donc réellement impossible de prouver quoi que ce soit puisque c'est "en général faux".
à moins que tu n'aies bouffé quelques phrases de l'énoncé avant...
Mon énonce ce résume qu'a cela, il ne manque rien j'ai re vérifier.
L'angle ABE fait 45° pour le coup, BAC doit 45°, y a t'il une propriété qui permettrait sachant cela pour démontrer que les droites sont parallèles ?
si tu affirmes qu'il n'y a réellement rien d'autre :
BAC n'a aucune raison de mesurer 45° vu que le triangle ACD est à priori quelconque et que rien dans la figure ni dans l'énoncé ne permet de dire qu'il serait particulier.
(que AB serait égal à BC, ou que l'angle C serait de 45° ou toute autre condition qui aboutirait à cette valeur d'angle là)
il suffit de déformer légèrement la figure (partir d'un triangle ABD différent) pour le "voir"
et la seule conclusion qu'on peut tirer est :
EB sera parallèle à AC si et seulement si l'angle ACD mesure 45°,
(ça c'est vrai et c'est tout ce qu'on peut en dire, on peut le prouver par les angles correspondants :
EB est parallèle à AC si et seulement si les angles DBE et DCA sont égaux)
mais avec les données de l'énoncé rien ne permet d'affirmer la valeur de cet angle
la propriété qu'on demande de démontrer est donc en général fausse.
point final.
D'accord c'est vrai qu'on peut rien affirmer ne sachant aucune donné ADC, merci beaucoup à vous tous de m'avoir aider.
on ne peut rien affirmer ne veut pas dire on ne peut pas faire l'exo !!
faire l'eco c'est écrire ce que j'ai dit (en ajoutant ton coup de la bissectrice à 45°)
on "fait" bien l'exo :
on démontre que la propriété qu'on demandait de démontrer est fausse...
ce qui est une conclusion tout aussi intéressante que si on avait pu démontrer qu'elle est vraie.
cela arrive tout le temps de "conjecture" une propriété, se dire "il me semble bien que ceci cela est vrai"
et quand on passe à la démonstration, on démontre finalement que cette belle propriété qu'on avait crue vraie est fausse.