Inscription / Connexion Nouveau Sujet
démontrer triangle isocèle dans parallélipipède rectangle
Bonjour à tous,
J'ai soucis pour démontrer qu'un triangle est isocèle
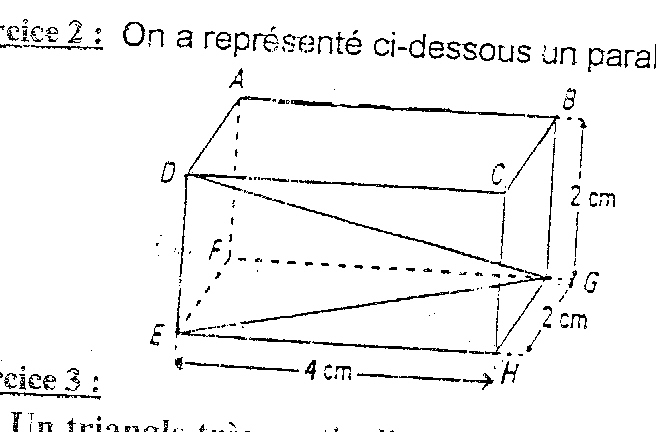
On a représenté un parallélipipède rectangle ABCDEFGH
Le triangle EGH est rectangle en H
Quelle est la nature du triangle DEG?
Je vois bien qu'il est isocèle en G mais je ne sais pas comment faire pour le démontrer.
Merci à celui ou celle qui voudra bien me mettre sur la voie....
bonne journée
Sam17
je pensais utiliser la symétrie mais je ne vois pas comment l'appliquer puisque le segment DG traverse le parallélipipède et que le segment EG est la diagonale du rectangle EFGH
les renseignements que tu donnes me paraissent bizarres,
pourrais-tu joindre le dessin du parallélépipède, STP
la procédure pour joindre une image est ici---->![]() [lien]
[lien]
Bonjour,
avec la figure, c'est beaucoup plus clair..
le triangle DEG n'est pas isocèle ..
c'est un triangle rectangle en E en effet le segment [DE] est perpendiculaire à [EF], [EH] et [EG]
Ah ouais... J'ai vraiment des problèmes dans l'espace. Je comprends la démonstration mais je n'arrive pas du tout à le visualiser rectangle. C'est extrèmement génant..
Je te remercie beaucoup pour ton aide...
Je te souhaite un très bon week end et peut être à bientôt
Sam17
pour essayer de visualiser les choses je t suggère quelque chose :
tu peux utiliser une boite en carton, sans couvercle, sur laquelle tu marques les sommets comme sur la figure, tu traces la diagonale [EG] sur le fond de la boîte et avec une ficelle tendue, tu essayes de matérialiser le côté [DG] du triangle DEG, tu verras alors que le triangle DEG est bien rectangle en E
Super comme idée. Je viens de le faire avec une boite à chaussure et là effectivement j'ai vu le triangle rectangle.
encore merci pour tout
Très bonne journée.
sam17