Salut,
Sans connaître g , ça me parait difficile...

Bonjour,

Je ne comprends pas : tu parles de f, et ensuite de g ?

Il manque des choses ...

Léo

bonjour,  a oui pardon j'ai oublié de donné le plus important f désigne une fonction vérifiant (f est définie et dérivable sur R et f(0) =1et f'(x)=f(x). soit g:x f(x)f(-x)

Et g ?

g(x)=f(x)f(-x)

f est définie sur , don g ...

donc g ....     voulais-je dire .

donc g est egalement définie sur

je comprend ou vous voulez en venir

... comme produit de fonctions définies sur le même domaine.

Et que vaut g(0) ?

g(0) vaut 1

mais c'est quoi le domaine? comment je le trouve?

g(0) vaut 1 car f(0)=1
dc f(0)f(-0)=1

mais c'est quoi le domaine?
==> tu me l'as donné à 17:42
comment je le trouve? ==> avec ce que je t'ai donné à 17:48

ok et donc g vaut bien 1 ou je me suis trompé?

Tu ne t'es pas trompé.

d'accord donc pour la 1ere question je dit que le domaine de définition de g c'est car c'est un produit de fonctions définie sur
et je fais mon calcule qui est égale à 1.
Merci.
et donc pour après la question 2 comment je fais, j'arrive pas voir ce que je doit faire.

Il faut dériver u.

donc u'(x)=...
je voit pas comment deriver f(-x)

[fog(x)]' = f'og(x)· g'(x) avec g(x)=-x

Léo : si xf(-x) a le même ensemble de définition que f, c'est parce que ce domaine est symétrique par rapport à 0

si par exemple tu avais une fonction f définie sur [-1;2], la fonction xf(-x) serait définie sur [-2;1] et g:xf(x).f(-x) ne serait définie que sur [-1;1]

et si f est définie sur ]0;1],... g n'est carrément jamais défini !

je comprend plus rien vous parler de quoi matheuxmatou?
je suis désolé mais en maths j'ai de très forte lacune et j'ai énormément de mal a vous comprendre

c'est Léo qui me posait une question sur cet exo et je lui réponds (j'ai indiqué que ma réponse lui était destinée en début de post)... donc n'en tient pas compte, merci (mm)

d'accord désolé.

léo c'est quoi la dérivée g'(x) et f'(x) je suis bloqué.

g  est dérivable sur comme produit de fonctions dérivables sur .

Et tu sais que (uv)'=u'v+uv'

_{Merci MM pour les éléments}

oui la formule je la connais mais je n'arrive pas a l'appliquer dans ce cas la.
(fog)'(x)=f'(x)o g(x) * g'(x)
mais après j'arrive pas a remplacer

. Il faut un minimum poser les choses de temps en temps pour avancer ...

f o h(x)=f(-x) avec h(x)=-x

et donc h'(x)=-1

d'où f'(-x)=[f o h(x)]' = f'o h(x)· h'(x) = f'(h(x)).h'(x) = f'(-x).(-1) = -f'(-x)

donc f'(-x)=-f'(-x)


. g(x)=f(x)f(-x)

On pose u=f(x) et v=f(-x)

Donc g(x)=uv

D'où g'(x)=(uv)'=u'v+uv'=f'(x).f(-x) + f(x).(-f'(-x))

sa répond a la question dériver u(x)=f(-x)?

Regarde la conclusion de à ma 5ème ligne ci-dessus.

f'(-x), c'est bien la dérivée de f(-x) non ?

oui, mais les h ils sortent d'ou?

Regarde la 2ème ligne de mon post de 19:07  ....

donc si je comprend bien u(x) = f'(x).f(-x) + f(x).(-f'(-x)) mais je n'est pas besoin de remplacer par des valeurs ? je peux laisser comme sa?

mais je n'est pas besoin de remplacer par des valeurs ? ==> remplacer quoi (?) par quelles valeurs au juste ?

, c'est ce qui est indiqué dans ton énoncé. Je ne vois donc pas pourquoi tu écris  u(x) = f'(x).f(-x) + f(x).(-f'(-x)) dans ton post ci-dessus.

On te demande de dériver u telle que u(x)=f(-x) ==> c'est ausssi ton énoncé

On a f o h(x)=f(-x) avec h(x)=-x et donc h'(x)=-1

d'où u'(x)= f'(-x)=[f o h(x)]' = f'o h(x)· h'(x) = f'(h(x)).h'(x) = f'(-x).(-1) = -f'(-x)

donc u'(x)=f'(-x)=-f'(-x)

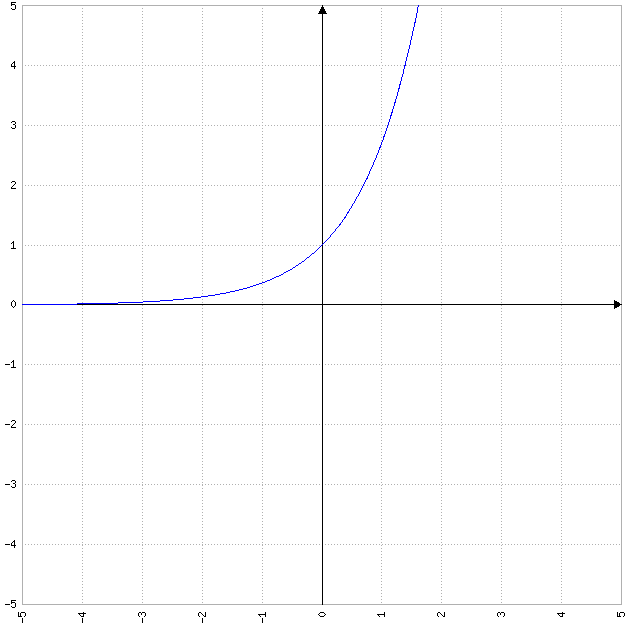
Ton exercice, c'est une introduction à l'apprentissage de la fonction exponentielle que tu verras très probablement prochainement, et dont la courbe est celle-ci.

Cette fonction est :

Et parra rapport à ton énoncé, on a  :







Et x , on a f(x) 0

Léo

Oui, c'est plus juste de mettre (f(-x))'.

Même si toutefois :

f(x) = e^x   ==> (f(-x))' = (e^-x)'= -e^-x = f'(-x)

ben non

Exact.

Je fini par m'emmêler ...