bonjour

1) erreur sur le calcul du discriminant, et donc revoir Df

comment justifies-tu que le domaine de dérivabilité est différent de Df ?

2) non
F(x) est un quotient de 2 fonctions, forme u/v
avec
u= ......            u ' = ..........
v= ......            v ' = ..........

et dans le cours on a : (u/v)' = .....

bonjour,

1) x1= (-b-c)/2a donc -b=2 c=-3 et a=0
qui est égal à 5 et x2= -1 c'est ça

2
u= -x²+2x+11    u'=-2x+2
v= x²-2x-3            v'= 2x-2

(u/v)' = ((-2x+2)*(x²-2x-3)-(2x-2)*(-x²+2x+11))/(x²-2x-3)²
après on développe et on réduit

1) a = 1 et non pas à 0   (sinon tu n'aurais pas de second degré )

ok pour la dérivée, continue

ps : à remarquer qu'au numérateur de la dérivée, on peut factoriser par (2-2x)

donc f'(x) = (-8x²-20x+16)/(x²-2x-3)²

ensuite pour connaitre le signe je sais que le (x-2x-3)² est positif et pour -8x²-20x+16 je fais le discriminant

pour -8x²-20x+16 je fais le discriminant dans quel but ? pour quelle question ?

ps : ça me fait penser que tu n'a pas clairement dit pourquoi tu cherches les racines de x²-2x-3  (écris-le sur ta copie)

f'(x) = (-8x²-20x+16)/(x²-2x-3)²   --- non, erreur quelques part
montre le détail si tu ne trouves pas ton erreur

j'ai fais une erreur de signe et je l'ai refais avec la factorisation de u' et v' et ça donne f'(x)=(-8x+8)/(x²-2x-3)²

sans mon erreur on résout -8x+8=0 pour trouver quand le fonction change de signe  

je trouve 8(2-2x)

donc f '(x) = 0 équivalent à 2-2x = 0 sur Df  --------  (tu as trouvé Df?)

Df sur \{-1;1}

non pour Df
reprends tranquillement tes calculs et montre les moi pour que je puisse t'aider

je sais plus comment on trouve Df

ah
on va rechercher les valeurs interdites de la fonction
ici, on n'a que le cas "dénominateur nul" à s'occuper (pas de racines carrées, pas de log)

donc on cherche les racines de x²-2x-3
on résout x²-2x-3 = 0
discriminant, etc.
... comme tu avais commencé à faire, mais sans les erreurs de calculs ^^
tu recommences ?

je m'absente un peu

je suis désolée malaurie1704 mais il me faut couper.
je reviendrai te lire plus tard, à moins qu'une personne ne prenne le relais.
a+

Df = \{-1;3}

c'est juste.

Merci beaucoup de m'avoir aider

avec plaisir
si tu veux me montrer ton tableau de variation, je te dirai s'il est ok.

Je pense que le deuxième est bon mais je ne suis pas sûre.

dis nous un peu comment tu étudies le signe de ta dérivée .....

_{bonjour Malou}

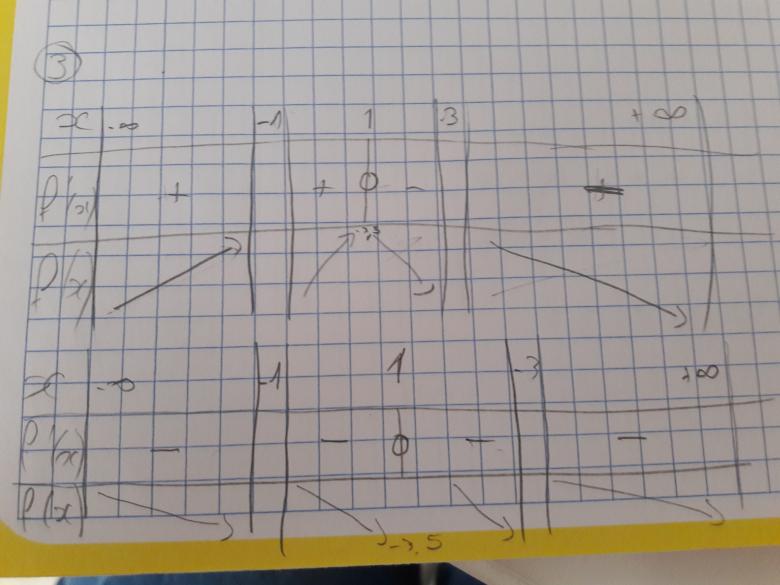
malaurie1704, effectivement, sur les 2 tableaux de variation que tu proposes,
un seul est juste.
pour en être convaincue - c'est ce qui est important! - , montre-nous stp comment tu étudies le signe de f'(x).

Pour étudier le single de f'. On sait que diviseur est positif donc le signe dépend de -8x+8

Donc j'ai résous-8x+8=0 qui m'a donner x=1

euh oui, f '(x) s'annule en 1, on est d'accord.
mais quel est le signe de f '(x) ? comment tu as fait ?

En regardant le signe de a

on avance...

-8x+8 est effectivement une forme affine
et le signe d'une fonction ax+b, on connait depuis longtemps :
voir si besoin le 4) de ce lien   Fonctions linéaires et affines

... et donc, quel tableau de variation tu valides ?

Le deuxième

stp, complète les signes sur le tableau suivant

+ 0 -

tout à fait
et tu m'as dit que f '(x) suit le signe de -8x+8, ce qui est exact.

re-donc.... quel tableau de variation pour f ?

Le premier

Merci beaucoup

oui, le premier.

bonne continuation