Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale DérivéesTopics traitant de Dérivées [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Dérivabilité d'une fonction racine n-ème

Posté par
Mathes1 06-12-20 à 15:16

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
Soit f la fonction numérique définie sur I=[-1;+[ par :
f(x)=x-\sqrt[3]{x+1}
a)Calculer \lim_{x \to +\infty } f(x)
b) étudier la dérivabilité de f à droite en -1 et interpréter graphiquement le résultat obtenu
c) Calculer f '(x) pour tout x]-1;+[ puis dresser le tableau de variation de la fonction f
Mes réponses
a) Calculons \lim_{x \to +\infty } f(x)
Transformation de l'expression puisqu'elle est une forme indéterminée , alors
x-\sqrt[3]{x+1}=\dfrac{x³-(\sqrt[3]{x+1})³}{x²+x\sqrt[3]{x+1}+(\sqrt[3]{x+1})²}=\dfrac{x³-x-1}{x²+x\sqrt[3]{x+1}+(\sqrt[3]{x+1})²}=\dfrac{x²(x-\dfrac{1}{x}-\dfrac{1}{x²})}{x²(1+\sqrt[3]{\dfrac{1}{x²}+\dfrac{1}{x³}}+\sqrt[3]{\dfrac{1}{x^4}+\dfrac{2}{x^5}+\dfrac{1}{x^6}})}=\dfrac{(x-\dfrac{1}{x}-\dfrac{1}{x²})}{(1+\sqrt[3]{\dfrac{1}{x²}+\dfrac{1}{x³}}+\sqrt[3]{\dfrac{1}{x^4}+\dfrac{2}{x^5}+\dfrac{1}{x^6}})}=\boxed{\red{+\infty}}
b)
\lim_{x \to -1+ } \dfrac{x-\sqrt[3]{x+1}-1}{x+1}=\lim_{x \to -1+ } (x-\sqrt[3]{x+1}-1)×\dfrac{1}{x+1}=\red{-\infty}
Donc f n'est pas dérivable en -1
Donc la courbe Cf admet une demi-tangente verticale à droite au point A(x0;f (x0)
Donc A(-1;1) dirigée vers le bas
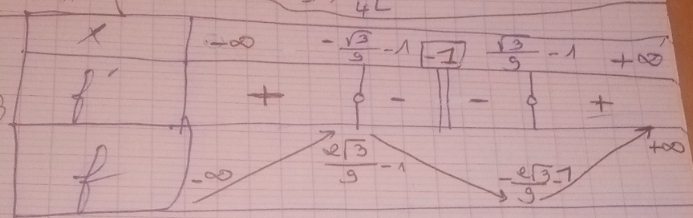
c)
f '(x)=(x-\sqrt[3]{x+1})'=1-\dfrac{1}{3\sqrt[3]{(x+1)²}}
Le dénominateur est strictement positif et -1<0 donc le quotient est négatif avec 1 >0
Donc f ' <0
Merci beaucoup d'avance

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 16:39

Bonjour

Merci beaucoup

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 17:03

Bonsoir, réponse très rapide, je ne pourrai reprendre avant 19h.

a) un peu compliqué. Tu peux  écrire:
racine cubique de x+1 = (racine cubique de x)*racine cubique de (1 + 1/x)
puis factoriser.

b) f(-1) = -1 donc f(x) - f(-1) = x - racine cubique de (x+1) + 1

c) f'(x) juste. L'étude de signe est fausse.

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 18:38

Bonjour
Merci beaucoup de m'avoir répondu
Pour a) je ne comprends pas comment factoriser :
x-\sqrt[3]{x+1}=x-\sqrt[3]{x}\sqrt[3]{1+\dfrac{1}{x}}
J'espère que m'a méthode est juste
b) oui vous avez strictement raison
\dfrac{x-\sqrt[3]{x+1}+1}{x+1}=\dfrac{x+1-\sqrt[3]{x+1}}{x+1}=\dfrac{x+1}{x+1}-\dfrac{\sqrt[3]{x+1}}{x+1}=1-\dfrac{\sqrt[3]{x+1}\sqrt[3]{(x+1)²}}{(x+1)\sqrt[3]{(x+1)²}}=1-\dfrac{\sqrt[3]{(x+1)^3}}{(x+1)(\sqrt[3]{(x+1)²}}=1-\dfrac{x+1}{(x+1)\sqrt[3]{(x+1)²}}=1-\dfrac{1}{\sqrt[3]{(x+1)²}}=\red{-\infty}
c) je ne comprends pas l'étude de signe
Une petite indication s'il vous plaît merci beaucoup d'avance

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 19:52

Rebonjour,

L'assistant latex ne veut pas me donner de racine cubique, grrr !! Cette fois-ci j'écrirai rc pour aller plus vite.

a) c'est juste. Ensuite tu peux factoriser toute l'expression par x ou bien par rc(x). Les deux marchent.

b) Là c'est bon, yes!

c)  je prends un peu plus de temps pour expliquer correctement. En attendant, regarde le a)

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 20:08

c) Je pense que tu n'as pas tenu compte du 1 devant l'expression négative :-1/rc((x+1)²)
Alors 2 possibilités :
Soit tu résous par exemple  l'inéquation f'(x) 0
Soit tu réduis au même dénominateur. Ce dénominateur est > 0, donc f'(x) a le signe du numérateur. Et tu te retrouves à un calcul du même genre que le précédent.

ça ira ?

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 20:24

Bonjour
Merci beaucoup de m'avoir répondu
Je n'arrive pas à factoriser pour a)
Pour c) d'accord
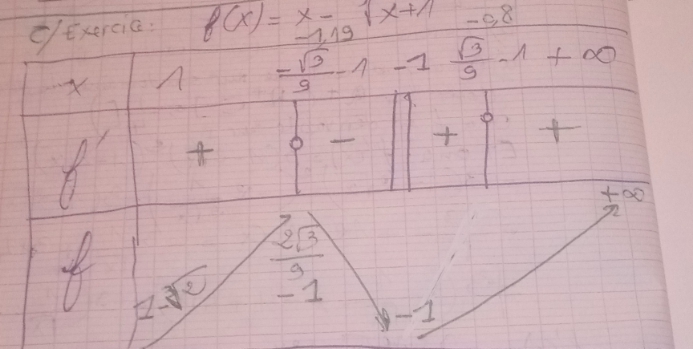
f '(x)=\dfrac{-1+3\sqrt[3]{(x+1)²}}{3\sqrt[3]{(x+1)²}}
Donc le signe de f ' est le signe de

-1+3\sqrt[3]{(x+1)²}
Merci beaucoup

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 20:45

Bonjour
Pour le tableau de variation ;
Dérivabilité d\'une fonction racine n-ème
Merci beaucoup

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 21:05

Attention, f est définie sur  [ - 1 ; +   [                                    

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 21:20

Bonjour
D'accord merci beaucoup
Dérivabilité d\'une fonction racine n-ème

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 21:26

Oh la la !! ce 1 en début de valeurs de x ??? Alors que 1 > - 1
Le tableau démarre à - 1. Tu supprimes tout ce que qui est inférieur.
D'accord ?

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 21:42

Bonjour
D'accord
Dérivabilité d\'une fonction racine n-ème
Merci beaucoup

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 06-12-20 à 23:27

Regarde l'ordre des nombres, ça ne va pas.
fatigué peut-être ? A reprendre plus tard.
Bonne nuit !

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 11:38

Bonjour
Merci beaucoup à vous !
Oui j'ai un peu fatigué hier , merci
Je pense qu'il y a un erreur dans l'énoncé
faite par l'énonciateur.

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 20:26

Bonsoir,

je n'ai pas vu d'erreur dans l'énoncé.

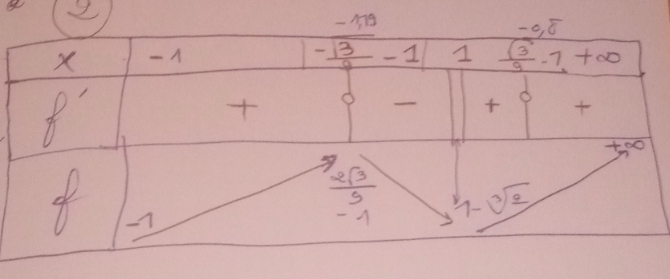
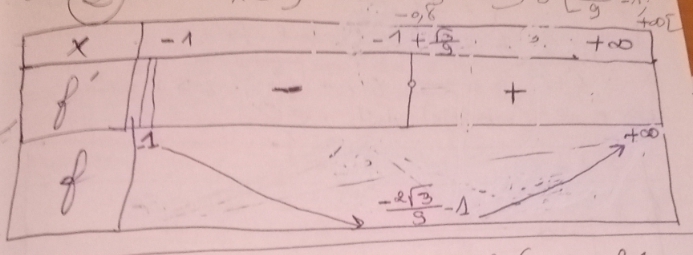
Je reprends ton dernier tableau de variations  ( ligne de x) :
- d'abord  - 1 - 3 / 9 < -1  donc ne peut figurer dans ce tableau pour lequel x [ - 1 ; + [
- ensuite tu écris que f' n'est pas définie en 1 et qu'elle change de signe. Ce n'est pas le cas. Il ne se passe rien de particulier en 1, aucune raison de signaler cette valeur.

La seule valeur de x qui intervient est - 1 + 3 / 9. Là effectivement la dérivée s'annule et change de signe.

Tu vois cela ?

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 21:56

Bonjour
Merci beaucoup de m'avoir répondu
Dérivabilité d\'une fonction racine n-ème

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 22:03

Attention, le signe la dérivée n'est pas bon. Il y a un changement de signe en - 1 + 3 / 9
Il serait bon que tu montres comment tu as procédé pour cette étude de signe ....

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 22:19

Bonjour
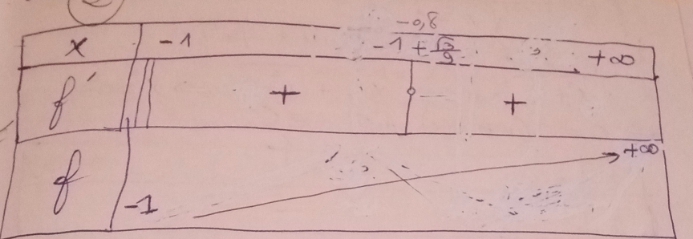
D'accord , je fais la compensation des nombres dans la fonction f '(x)
Par exemple dans -1 jusqu'à -1+\dfrac{\sqrt{3}}{9} j'ai choisi -0,5 ,-0,6,-0,7 pour les compenser dans f ' , je trouve des nombres positif , la mêmes choses pour l'autre côté .
Merci beaucoup

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 22:28

Essaie donc - 0,9
Il faut faire une étude plus rigoureuse de signe de f'(x). Cf mon message d'hier à 20h08

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 22:45

Bonjour
Je résoudre donc l'inéquation f '(x)≥0
Je trouve
x]-\infty;-\dfrac{\sqrt 3}{9}-1]{\bigcup{}}[\dfrac{\sqrt 3}{9}-1;+\infty[
Donc
Dérivabilité d\'une fonction racine n-ème
Merci beaucoup

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 23:02

Oui !!!
Je n'ai juste pas vérifié la valeur du minimum.

Posté par
Mathes1re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 23:10

D'accord
Merci beaucoup à vous
Bonne nuit !

Posté par
co11re : Dérivabilité d'une fonction racine n-ème 07-12-20 à 23:26

Bonne nuit aussi
le minimum a l'air bon. Waouhh!


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1677 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !