Inscription / Connexion Nouveau Sujet
Dérivation "
Bonjour j'ai besoin d'aide pour certaines des question de mon exo svp
Répondez par V (Vrai) ou F (Faux)
1. La courbe représentative de la fonction f ci dessous permet de dire que :
a) f est impaire
b)f'(-1)=1
c) existe et est comprise entre 10 et 15.
d) l'équation f(x)=0 n'as pas de solutions.
d) La dérivée f' est croissante sur l'intervalle [-2;-1].
e) Le coefficient directeur de la tangente en 1/2 est égal à 10.
f) Quand x, la courbe de f est en dessous de sa tangente en tout point.
g) f s'annule deux fois.
h) Si f(x) est un polynôme ,il est au moins de degré 4
i) La tangente en -1 a un coefficient directeur négatif
j) Il n'existe aucun point de Cf d'ordonnée inférieure à 30 .
k) L'équation f(x)=20 a deux solutions sur [-2;2]
l) La fonction f admet un extremum relatif en 1
m) f(2)=60
a) Faux car la courbe de Cf n'est pas symétrique par rapport à l'origine du repère.
b)
c)
d) Faux car la courbe coupe deux fois l'axe des abscisses
e)
f)
g)Vrai car la courbe coupe deux fois l'axe des abscisses
h)
i)
j) Vrai
k) faux cette équation a deux solutions mais pas dans [-2;2]
l)
m) Faux ,on pas savoir
Bonjour,
a) faux : tu as raison
b) faux : f'(-1) est le coefficient directeur de la tangente en x = -1, ce coefficient vaut 2
c) faux : f(0) existe et est non nul, cette limite est infinie, et elle dépend du sens par lequel x -> 0
d) : faux, tu as raison
Attention, tu as deux fois d)...
d) : vrai, la concavité de la courbe est tournée vers le haut sur l'intervalle
...
Bonjour
La courbe représentative de la fonctionci-dessous permet de dire que :
a) est impaire Faux
b)f'(-1)=1 Quel est le coeff directeur de la tangente en -1
c)\ existe et est comprise entre 10 et 15.
d) l'équation n'a pas de solutions.y a-t-il des tangentes parallèles à l'axe des abscisses
d) La dérivée est croissante sur l'intervalle [-2;-1]. Quel est le signe de la dérivée seconde
e) Le coefficient directeur de la tangente en 1/2 est égal à 10. Tracez la tangente en 1/2 et regardez
f) Quand], la courbe de
est en dessous de sa tangente en tout point.
g) f s'annule deux fois. vrai
h) Si est un polynôme, il est au moins de degré 4 combien de fois s'annule la dérivée
i) La tangente en -1 a un coefficient directeur négatifvoir b
j) Il n'existe aucun point de Cf d'ordonnée inférieure à 30. Que vaut f(1)
k) L'équation a deux solutions sur [-2 ;2]
l) La fonction f admet un extremum relatif en 1 Que vaut f'(1)
m)
Le nombre dérivé en un point est le coefficient directeur e la tangente à la courbe en ce point
Cela revient donc à lire l'équation de la droite.
10: 16 Que voulez-vous dire ?
N'y a-t-il pas un bandeau avant la courbe précisant certains points. Le repère est tel que l'on ne peut lire le graphique qu'avec très peu de précision.
Je dirais plutôt 40 Le point d'intersection avec l'axe des ordonnées aurait comme coordonnées et le point de tangence
soit
avec
la fonction dont la courbe est donnée et
celle définie par
et
étant continues ou dérivables en 0 on a donc
On est donc amené à déterminer la limite en 0 de le numérateur tend vers une limite finie
et le dénominateur vers
donc le quotient tend vers l'infini
pour d) f a deux solutions car la courbe touche deux fois l'axe des abscisse mais j'ai pas compris ce que vous avez dit
Pourquoi ?
La courbe coupe bien deux fois l'axe des abscisses,
l'équation a deux solutions
J'avais lu au temps pour moi
Il faut lire le coefficient directeur de la tangente Il semble que pour 1/2 la courbe admette un maximum local Comment est alors la tangente ?
Lequel d ?
second d
La dérivée seconde est positive sur car la courbe est au dessus de ses tangentes donc concave
Certes il n'y a qu'une tangente tracée mais on peut envisager d'en tracer maintes et alors on verrait que la courbe serait toujours au dessus par conséquent que la dérivée seconde serait positive donc la fonction dérivée croissante sur cet intervalle
Comment faire pour la voir sur le graphique ?
OK sinon comment je fais ça?👆Samsco
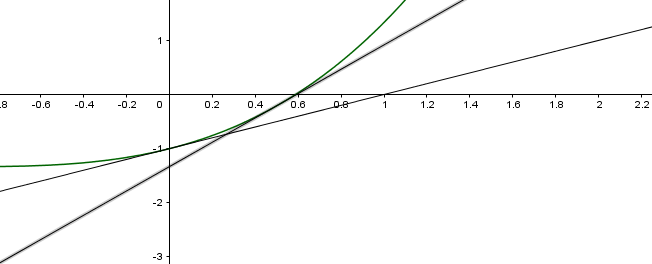
On peut voir sur cette partie que toutes les tangentes ( j'en ai tracé 2) sont en dessous de la courbe
par conséquent ce qui implique que la dérivée de
est croissante
IL en est de même sur le graphique donné sur l'intervalle [-2~;~-1]
J'ai bien compris ce que vous vounez de faire là mais le problème ,c'est je vois pas comment tracer plusieurs tangente ,je peux place qu'une seule
Il y a une tangente en chaque point mais pour chaque valeur de la tangente si on la dessinait serait en dessous de la courbe
regardez-ici par exemple vers la fin
Oui c'est bien ce que l'on veut si la fonction est convexe( ici simple lecture) alors on peut en déduire que la dérivée seconde est positive et par conséquent la dérivée première est croissante.
Oui je vois moi je sais pas comment tracer plusieurs tangentes pour voir plus claire ce que vous dites
En -1,9 , je ne vois pas de point de tangence et est ce c'est mm ordonnée à l'origine qu'on utilise ?
Dans la mesure où vous n'avez pas l'équation de la courbe ou la définition de la fonction on ne peut pas écrire explicitement l'équation de la tangente. On essaie de la tracer la mieux possible
et ici on verrait que cette tangente est toujours en dessous de la courbe.
Sur un cercle vous pouvez bien tracer en n'importe quel point une tangente. pour une courbe c'est identique
Cela vous sera peut-être plus parlant vous voyez bien que l'on peut tracer une tangente en chaque point et ici elle reste bien en dessous de la courbe
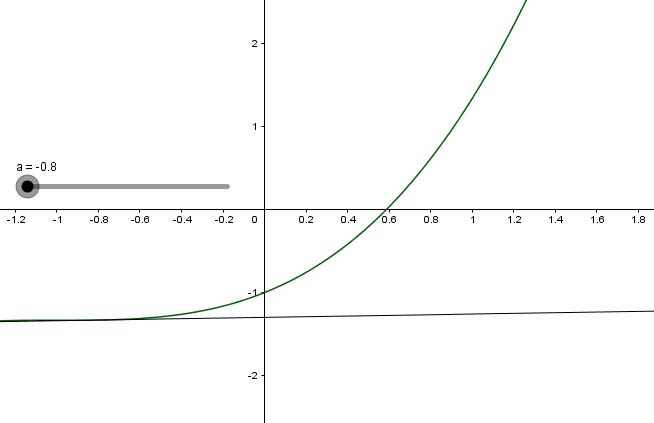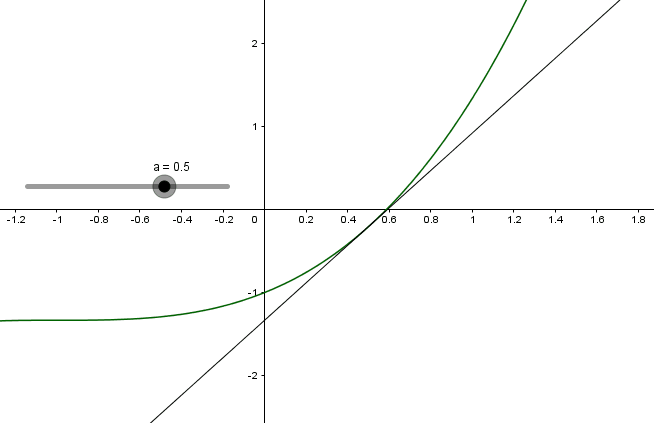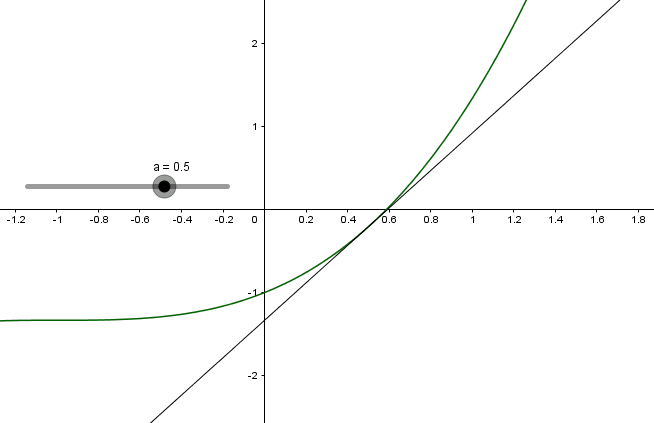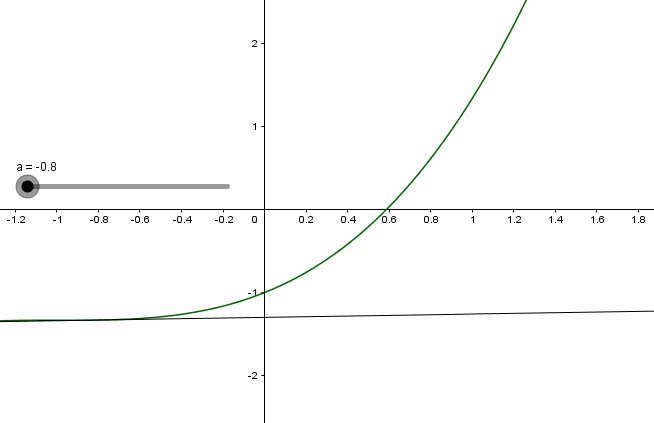
A vrai vrai dire ,je ne sais pas tracer une tangente ,je sais qu'on la trace au point A(a ; f(a)) mais bon je ne sais pas comment
Deux cas possibles
Si l'on connaît l'équation on est ramené à tracer une droite
Si l'on ne la connaît pas on essaie de tracer une droite touchant la courbe le plus possible
Annuler
connectez vous