Inscription / Connexion Nouveau Sujet
derivation
Bonjour,
J'ai besoin de votre aide. Je suis bloqué sur la question 2.
On considère la fonction f définie sur ]0; +∞ [ par f(x) = a√x + bx²+ c/x où a, b et c sont trois réels.
On note Cf la courbe représentative de f dans un repère.
1. Déterminer l'expression de la dérivée de f en fonction de a, b et c.
2. Déterminer a, b et c pour que Cf passe par le point A(4; 49) et que la tangente à Cf au point
d'abscisse 1 ait pour équation : y = −x + 2.
Piste : On peut s'aider d'un système d'équations pour la question 2.
Merci bcp de votre aide
Bonjour,
Oui, c'est ça.
Maintenant il faut utiliser les indications.
Tu as f(4)=49. Quelle équation cela te donne t il ?
 extrait de
extrait de Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
écris avec / pour diviser et utilise des parenthèses

malou edit > balises LTx rajoutées, bravo pour l'essai, tu y es presque , et tu peux aussi utiliser l'éditeur Ltx, celui avec les 3 petits points rouges en dessous
Il faut que je trouve une equation de la tangente qui donnait -x+2
-x+2 = f'(a)(x-a)+f(a)
Ça donne
-x+2 = -1 (x-1) +(1)
Donc f'(1)= -1 et f (1) = 1
Je dois déterminer mtn a b et c pour que Cf passe par le point A(4.49)...
Tu as déjà cette équation. Voir ton message de 11h31.

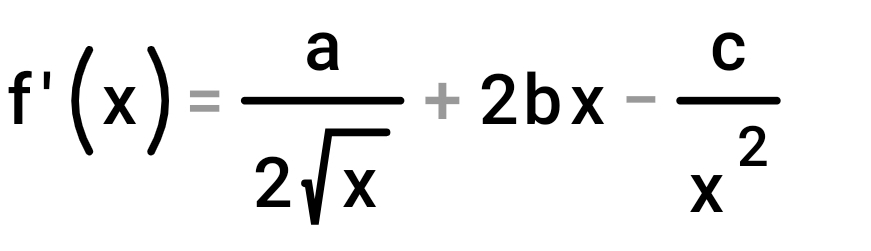
 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
 4 = ?
4 = ?

