Inscription / Connexion Nouveau Sujet
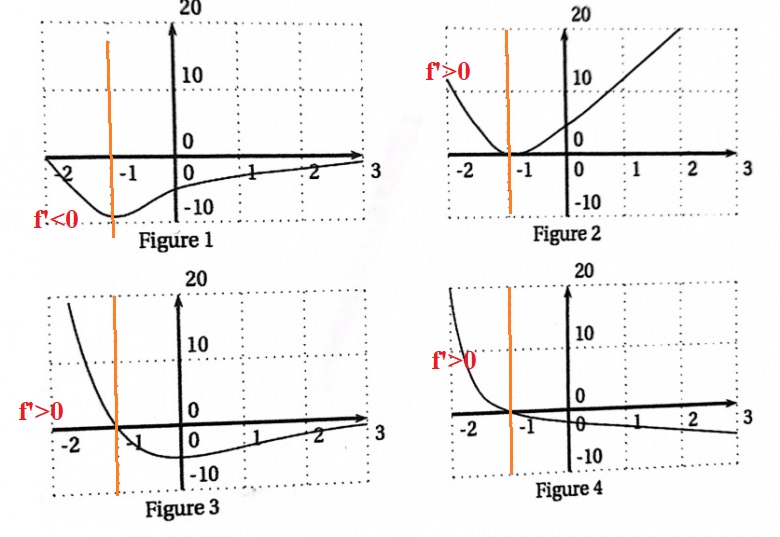
Donc maintenant il me reste plus que la figure 3 et 4, j'ai éliminé les deux premières figures car dans la figure 1, sur [-2;1[la f' est négative donc ce n'est pas bon.
On ne peut par ce raisonnement éliminer que la figure 1, pas la 2.
Merci beaucoup, vraiment.
C'est la première fois que j'utilise cet application et je suis heureuse de discuter avec une personne agréable comme vous.
Merci beaucoup, ce que vous écrivez est très clair et détaillé.
Je vous souhaite une bonne soirée. 
Ah bah mince, je croyais que je suis sur le bon chemin.
Alors du coup, ce n'est toujours pas clair pour moi.
Alors pour la figure 2, j'élimine car disons que sur ]-1;0[ f' est positif ?
A partir de -1, ta fonction ne fait que décroitre, donc sa dérivée
à partir de -1 sera toujours ....
..... et donc si elle est toujours négative, son graphe doit obligatoirement rester sous l'axe des x.
Ce qui élémine donc la figure n° ...
Oui j'avais déjà compris, je crois que j'ai mal expliqué.
Je voulais dire que on remarque dans la figure 2, que la f' est positive donc ça ne correspond pas à la fonction f car son dérive f est toujours négatif.
Désolée, j'ai mal expliqué.
Voilà, tout est donc bon.
Donc pour la figure 3 et 4, j'élimine la figure 3 car bien que la dérivé f est négative, mais elle monte. Donc c'est la figure 4 qui représente.
J'espère que je suis claire.
Merci
Donc pour la figure 3 et 4, j'élimine la figure 3 car bien que la dérivé f est négative, mais elle monte. Donc c'est la figure 4 qui représente.
Je pense que là tu vas trop vite en besogne.
Aaaaah c'est bon en plus, on remarque dans la figure 3, la courbe ne commence pas par l'axe d'abscisse 2, alors la définition est [-2;3], comprenez vous que j'essaie de dire ?
Non.
l'axe d'abscisse 2
alors la définition est [-2;3]
comprenez vous que j'essaie de dire ?
C'est compliqué d'expliquer.
Je veux dire que l'ensemble de définition de la fonction f est [-2;3] on est bien d'accord ?
On remarque sur la figure 3, l'ensemble de définition n'est pas représentée.
C'est plus clair ?
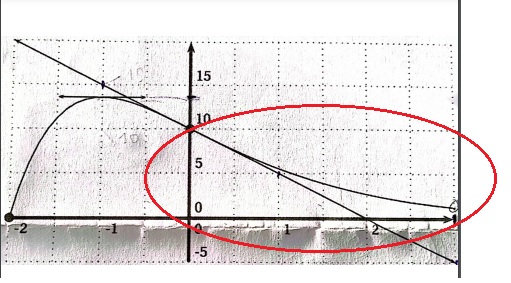
Cela t'induit en erreur. Le domaine de définition ne te sera d'aucune utilité ici, il s'agit là "d'extraits" de fonction dont le domaine de définition est très certainement
La question à te poser à présent, c'est "que fait ta fonction sur la seconde partie entourée en rouge" ?
Je suis désolée si je repond tardivement, j'étais occupée et c'était pas prévu.
Je vous remercie beaucoup et bonne soirée.