Inscription / Connexion Nouveau Sujet
Dérivation
Bonjour,
D'habitude, j'arrive à donner les variations de f à l'aide du graphique.
Mais cette fois-ci, je n'y arrive pas car je n'arrive pas à préciser l'ordonnée.
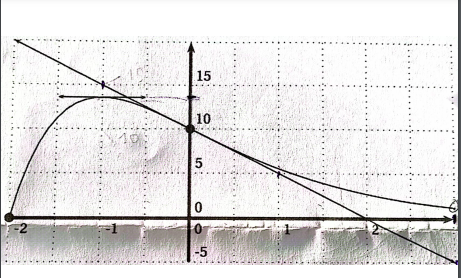
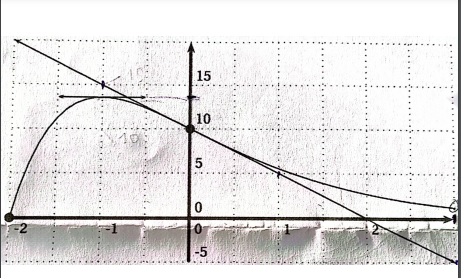
La courbe ci-dessous ( ci-joint) représente une fonction f définie sur [-2;3]
1) donner une équation de la tangente au point d'abscisse 0.
( réponse trouvée <=> y =5x+25 )
2) Donner les variations de f.
Ce que j'ai trouvé : sur [-2;-1[ f est croissant et que f(-2) =0 et f(-1)=?, je n'arrive pas à trouver ce nombre entre 10 et 15 sur l'axe des ordonnés. Ce n'est pas 14 ?
Et puis je me demande si la réponse du 1 a le rapport avec le 2 ?
Merci d'avance.
Bonjour, merci de votre attention.
J'ai pourtant mis et ça n'a pas fonctionné. Je refais .
Pourriez vous me dire si c'est bon.
pour insérer un graphique, suis les consignes après avoir appuyé sur le bouton "Img" situé sous le cadre
1) l'équation que tu as trouvée(y =5x+25 ) est fausse
tu peux vérifier facilement en utilisant le graphique:
si x=0 que vaut y ?
si y=0 que vaut x?
f(0)=10
Donc f'(0) est le coefficient directeur de la tangente à Cf au point d'abscisse 0.
f'(0) = ya-yb/xa-xb = 10-15/0-(-1) = -5
Équation de la tangente :
y=f'(a)(x-a)+f(a)
<=>y=-5(x-0)+10
<=>y=-5x+10
Oui effectivement j'ai mal calculé. Merci.
Désolé Pirho (et bonjour), je croyais que tu étais sparti.
ce n'est rien . Je dois quitter pendant une heure.
Peux-tu poursuivre?
Pourquoi ce n'est pas bon ?
Pourtant j'ai vérifié, si x=-2 alors y=5*(-2) +10 = 0 et ça correspond bien à la graphique.
est l'équation d'une droite dont le coefficient directeur est égal à (-5), ce qui veut dire graphiquement que :
- quand on avance de 1 horizontalement
- on descend de 5 verticalement
Est-ce le cas sur ton graphique ?
Ce n'est pas grave.
Pour le 2, donner les variations de f, je n'y arrive pas. Je sais que sur ]-2;1[ f est croissant et que f(-2)=0 mais pour f(-1) =? Je trouve pas son ordonné. C'est pas précisé sur graphique.
Je sais que sur ]-2;1[ f est croissant
C'est exact.
Que remarques-tu ensuite pour ta courbe ?
Nous nous demandons si ce n'est pas grave si le chiffre qu'on a choisi dans l'ordonnée n'est pas précis pour calculer l'équation de la tangente ?
Oui mais le problème, j'ai besoin de savoir l'ordonnée de -1.
Mais apres sur ]-1;3] f est décroissant. Mais il faut savoir des ordonnés pour compléter le tableau mais sur la graphique, c'est pas trop précise.
Oui mais le problème, j'ai besoin de savoir l'ordonnée de -1.
Pourquoi penses-tu avoir besoin de cette valeur ?
Parce que je fais toujours ceci avec mon prof, il faut savoir ces valeurs pour compléter le tableau.
Si vous allez me dire que c'est inutile, alors je vous suis. Donc c'est juste : sur ]-2;-1[ f est croissant et sur ]-1;3] f est décroissant.
est ce suffisant ?
Merxi.
louis222, tu déboules sans crier gare dans une discussion ouverte par quelqu'un d'autre
La moindre des politesses serait de demander aux personnes présentes si cela ne les dérange pas, et de respecter les questions posées par l'initiateur de la discussion
On pourrait dire que c'est suffisant, mais ce qui m'embête, c'est cela :
D'habitude, j'arrive à donner les variations de f à l'aide du graphique.
Mais cette fois-ci, je n'y arrive pas car je n'arrive pas à préciser l'ordonnée.
qui me laisse à penser que tu confonds certaines choses.
Je pensais que pour donner la variation de f, il est obligé de savoir les ordonnés.
Mais finalement non. Je suis convaincue merci.
Je peux encore poser la question pour la suite ?
Merci beaucoup.
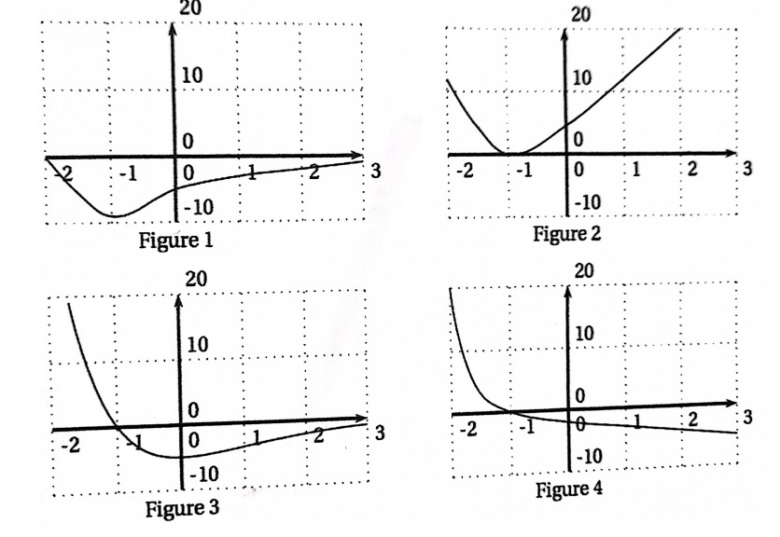
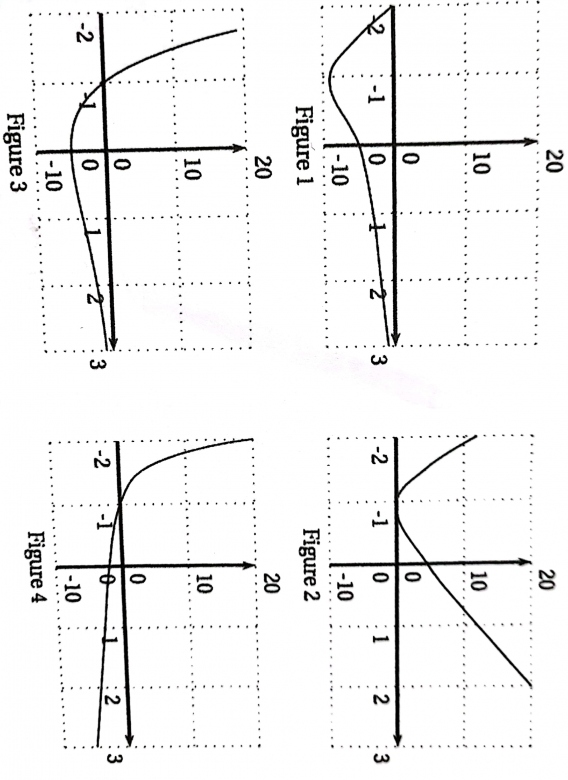
Le 3) une des 4 courbes ci-dessous représente graphiquement la fonction f'.
Déterminer celle qui la représente en justifiant l'élimination de chacune des 3 autres courbes.
Je suis désolée si j'ai mis de temps.
Merci
Dans ce cas là, il faut connaître le signe de f' pour pouvoir facilement répondre à cette question. Sur ]-2;-1[ est positif et sur ]-1;3] est négatif .
Et je ne vois pas que ça correspond à ces graphiques, la courbe au départ ne fait que descendre.
Dans ce cas là, il faut connaître le signe de f' pour pouvoir facilement répondre à cette question.
Oui, mais tu confonds "signe" et "variation".

Avec mon prof, on complète la variation de f et pour trouver f', il faut toujours mettre le signe c'est à dire positif ou négatif.
C'est ce qu'on fait actuellement.
Tu confonds fonction positive avec fonction croissante.
Voici l'exemple d'une fonction telle que
pour t'illustrer ta confusion.

Oh merci, vous avez raison, je pense que je n'avais pas bien compris les cours. Car je croyais que si f est croissant donc forcément c'est positive.
Merci, je vais réfléchir et je reviens.
Merci beaucoup.
Je suis là, impossible de comprendre. D'après ces graphiques, la figure 1, on remarque que la courbe est toujours négative]-2;1[ f est décroissant donc c'est pas bon.
Puis la figure 2,
La courbe est positive mais toujours décroissante et les suites les courbes sont toujours décroissante.
Comment résoudre ?
Merci.
Je te remets mon exemple avec cette fois_ci la fonction exemple en rouge, et sa dérivée en bleue.
Regarde bien la correspondance entre les 2.
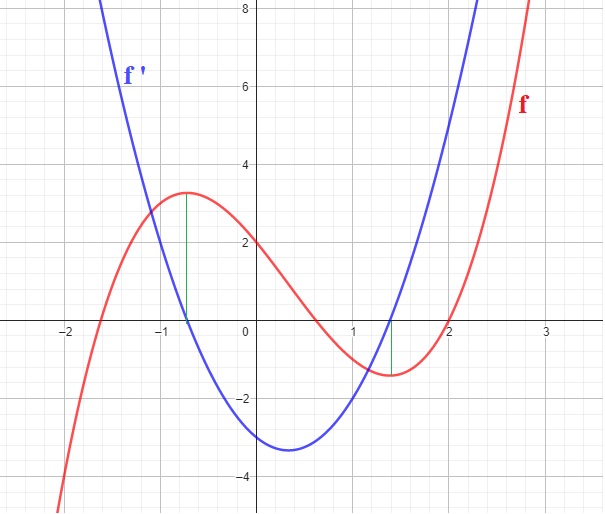
Donc c'est la figure 4 qui représente puisque d'après votre exemple, on remarque que la courbe f monte au départ et la courbe f' descend mais sur ]0;+infini[ les courbes montent simultanément.
Mais comment justifier pour éliminer le reste, auriez vous une chapitre à me montrer pour rédiger ? Car je crois que je ne comprends pas trop vraiment. Pourquoi lorsque f est croissant au départ et que f' est forcément décroissant ?
Merci.
Sur ]-2,-1[, ta fonction f est croissante, donc sa dérivée f' doit être positive.
Donc sur le graphique de la dérivée, entre -2 et -1, ta courbe doit etre au-dessus de l'axe des x, sinon, cela voudrait dire qu'elle est négative, et donc que ta fonction d'origine serait décroissante.
A partir de là, tu dois déjà être capable d'éliminer celle ou celles qui ne corresponde(nt pas.
Ah mais c'est très clair, merci beaucoup.
Donc maintenant il me reste plus que la figure 3 et 4, j'ai éliminé les deux premières figures car dans la figure 1, sur [-2;1[la f' est négative donc ce n'est pas bon.
Et dans la figure 2, sur ]-1;3] la f' est positive ce qui n'est pas le cas.
Et maintenant dans la figure 3, tout est bon mais la courbe monte donc la figure 4 représente ?
Merci beaucoup, je comprends beaucoup mieux. A part pour les deux restes la figure 3 et la figure 4.