Inscription / Connexion Nouveau Sujet
Dérivé
Bonjour, je suis en terminale. Je dois réaliser un exercice portant sur des révisions de première mais j?ai un peu de mal.
Voici l?énoncé :
Dans chaque cas, on considère une fonction f définie sur l?intervalle I. Construire le tableau de variations de f sur I.
1) f(x)=1/3x3-x2-3x+1 sur I=[-3;6]
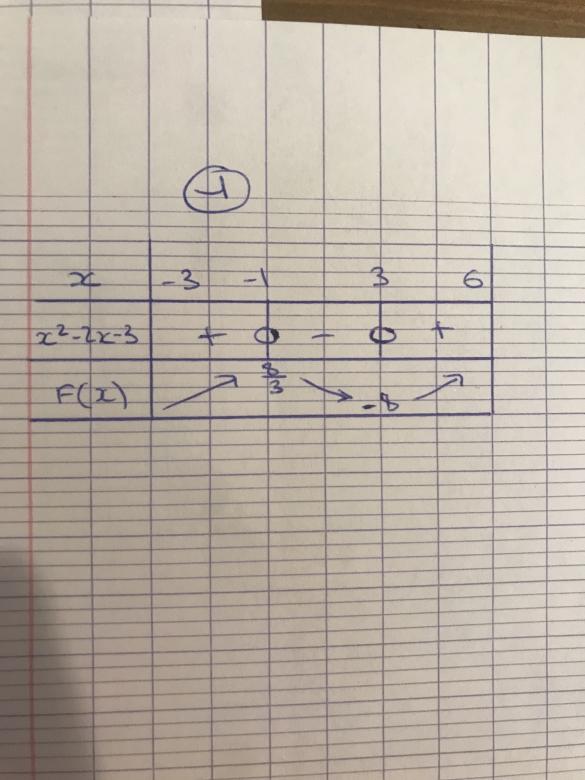
Donc j?ai calculé la dérivée qui donne : f?(x)=x2-2x-3 et j?ai donc calculer le discriminant qui est égal à 16, donc la fonction a deux solutions: x1=3 et x2=-1. å>0 donc la parabole est tournée vers le haut. Le tableau de variations est mit en bas (1)
2) f(x)=(2x-1)/(x2+1) sur I=[-2;4]
Donc je calcule la dérivée de la fonction qui donne:
f?(x)=(u?*v-u*v?)/v2
f?(x)= (-2x2+2x+2)/(v2+1)2
(je détaille pas les calcules car vraiment long a taper...)
Je calcule le discriminant qui donne 20, donc la fonction a deux solutions:
x1=(1-V5)/2 et x2=(1+V5)/2
a>0 donc la parabole est tournée vers le haut.
Cependant je n?arrive pas à savoir comment calculer la valeur interdite de la fonction f, qui est: v2+1 n?est pas egal à 0
J?enverrais le tableau de variations une fois avoir trouvé la valeur interdite ..
Bonjour olidbr
mets ton profil à jour s'il te plaît, merci !
Bonjour,
Si tu es en terminale, mets à jour ton niveau dans ton profil, s'il te plait.
Pour 1), ce n'est pas la fonction qui a 2 solutions, c'est la dérivée qui s'annule pour 2 valeurs de x.
En terminale, on ne parle plus de parabole pour le signe d'un polynôme de dgré 2, mais d'une règle. Genre :
Le trinôme est du signe du coefficient de degré 2 à l'extérieur de ses racines.
Pour 2), idem. C'est le numérateur de la dérivée, et pas la fonction qui s'annule 2 fois.
Le dénominateur n'est pas (v2+1)2 mais (x2+1)2.
Ceci n'est pas clair du tout :
calculer la valeur interdite de la fonction f, qui est: v2+1 n'est pas egal à 0
Pourquoi veux-tu qu'il y ait une valeur interdite ? il peut ne pas y en avoir.
C'est la cas ici, car le dénominateur x2+1 n'est jamais nul.
Essaye d'utiliser ces mots : dérivée, numérateur, dénominateur pour désigner ce dont tu parles.
Au lieu d'écrire "fonction" pour tout.
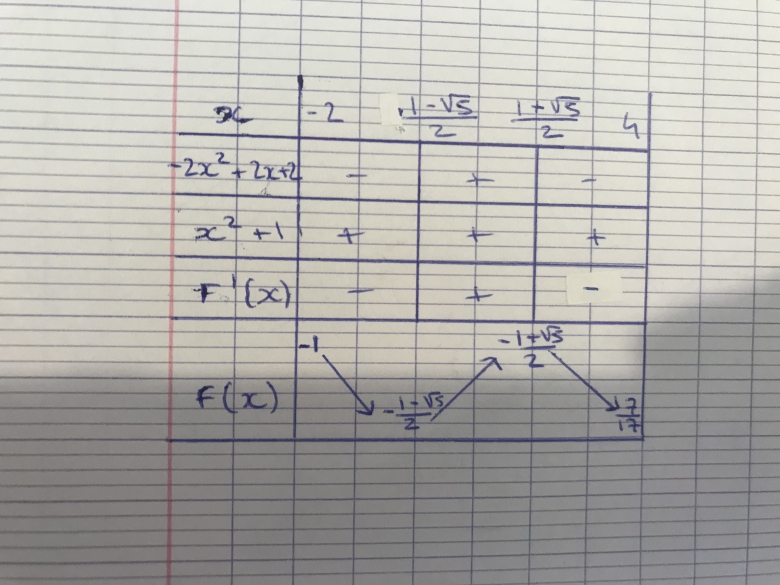
Q1 : tes calculs sont justes , montre ton tableau.. (ou explique le)
Q2 : tes calculs de dérivée sont corrects aussi.
attention ici a est <0 (a=-2)
ta question :
x²+1 = 0
x² = -1 qu'en conclus tu ?
Bonjour,
si x2 = -1
l'affirmation est fausse donc x n'appartient pas aux réels ?
Si c'est bien ça, comment je l'explique dans le tableau?
olidbr,
ton tableau est bien, tu peux le compléter avec les valeurs de f(-3) et f(6).
D'accord, merci !
x² = -1 n'a pas de solution dans R , donc pas dans ton intervalle d'étude.
ton dénominateur ne s'annule jamais : il n'y a pas de valeur interdite.
(tu ne mets donc pas de double barre dans ton tableau).
* Modération > Citation inutile effacée. *
Ah d'accord, donc je ne représente pas de ligne pour x2+1 dans mon tableau puisqu'il n'est pas dans mon intervalle, c'est bien ca?
inutile de citer mes messages, nous sommes deux..
"donc je ne représente pas de ligne pour x2+1 dans mon tableau puisqu'il n'est pas dans mon intervalle, c'est bien ca?"
tu ne lis pas bien ce que je te dis.
tu demandais quelle était la valeur interdite : il n'y en a pas, car x²+1 ne s'annule pas dans R. Donc pas de double barre dans le tableau.
maintenant tu me parles de ligne x² + 1 dans le tableau.. c'est différent.
et dire "x²+1 n'est pas dans mon intervalle" est faux.
olidbr, tu n'es pas nouveau sur ce site : tu sais bien que seules les photos de figure sont autorisées.
la prochaine fois tape ton tableau (avec latex, c'est mieux), ou explique le. C'est rapide.
Pour terminer sur ce topic : ta dérivée est bonne, le signe de la dérivée est correct dans ton tableau, les variations (flèches) de la fonction sont correctes aussi ; je n'ai pas vérifié tes calculs pour les images..
@Leile,
olidbr n'est pas banni pour les images de ses tableaux, mais pour ne pas avoir mis à jour son niveau dans son profil 
Les images de tableaux sont tolérées. Sinon elles auraient été effacées 
ah bon, on est banni quand on n'a pas actualisé son profil ? Je ne savais pas que c'était un motif de banissement..