Inscription / Connexion Nouveau Sujet
Dérivée
 Dooha
DoohaBonjour,
J'ai pas compris un exercice, pouvez-vous m'aider?
Exercice:
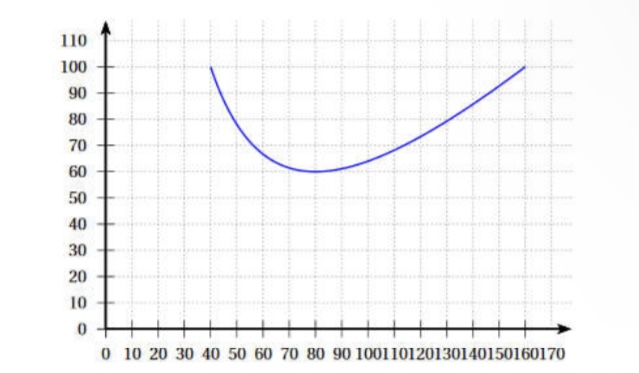
Soit f la fonction définie sur l'intervalle [40;160] par f(x)= x -100 +6400/x
La courbe ci-dessous est la représentation graphique de dans un repère.
1. Calculer la dérivée f' de f est montrer qu'elle peut s'écrire : f'(x)= x² -6400/x²
2. Étudier le signe de f'(x) sur l'intervalle [40;160]
3. En déduire le tableau de variation de f sur l'intervalle [40;160]
4. Le coût exprimé en F, de x repas préparés par service dans un restaurant, peut s'écrire, pour x ∈ [40;160]:
C(x)= x² -100x +6400
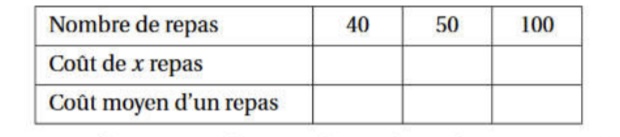
a. Compléter le tableau: ci-dessous
b. Écrire le coût moyen d'un repas en fonction du nombre de x de repas préparés. On notera ce coût moyen unitaire Cm(x).
c. Déduire de la question 3. Le nombre de repas que ce restaurant doit servir pour que le coût moyen d'un repas soit minimal.
d. Trouver à l'aide du graphique, à quel intervalle doit appartenir x pour que le coût moyen unitaire soit inférieur ou égal à 90 F.
Merci pour l'aide.
salut
il n'y a pas à comprendre il y a à faire ...
ne sais-tu pas calculer la dérivée d'une fonction ?
(les trois premières questions sont vues dès la première)
et quel est le lien entre la fonction f et la suite de l'exo ?
ne manquerait-il pas un bout d'énoncé ?
Bonjour
Il ne faut pas oublier les parenthèses
en ligne cela s'écrit
(x^2-6400)/x^2
Que proposez-vous ? Qu'est-ce qui vous pose problème ?
4 b On ne peut considérer C(x) le coût de repas et C(x) son coût moyen. N'écrivez pas d'homonymies
Il manque encore les parenthèses. Il n'y a pas que 6400 à être divisé par
coût moyen
Le tableau de la question 4 ?
Vous calculez le coût pour la quantité de repas proposé et vous divisez ce coût par cette quantité
Si le coût de 3 tablettes de chocolat est 6 euros. Le coût d'une est
Pour être plus précis
le coût de 40 repas par 40
le coût de 50 repas par 50
le coût de 100 repas par 100
4 b) c'est la même question que 4 a généralisée
4 c) quel est le minimum de f ? Pour quelle valeur ?
4 d) Lecture graphique


