Inscription / Connexion Nouveau Sujet
Dérivée
Bonjour,
Je souhaite avoir de l'aide concernant un exercice sur la dérivée.
Voici l'exercice :
Soit la fonction f définie par : f(x)= 4x/x²+1 sur [-3;3]
a) Déterminer l'expression de f'(x)
b) Dresser, en justifiant le tableau de variation de f
c) Déterminer deux nombres réels m et M tels que, pour tout réel x de [-3;3], on a :
m
f(x)M
d) Résoudre graphiquement, à l'aide de la calculatrice, la courbe représentative de la fonction f. Résoudre graphiquement l'équation f(x) = 1. Retrouver le résultat algébriquement.
Voici ce que j'ai fait à présent :
1) f(x)'=u'*v-u*v'/v²
u(x)=4x u'(x)=4
v(x)=x²+2 v'(x)=2x
f'(x)=4x*x²+2-4x*2x/(x²+2)²
f'(x)=4x²-8x²/x^4+4
f'(x)=-4x²/x^4+4
Merci d'une réponse.
Bonjour,
1) La fonction que tu as donnée n'est pas correctement écrite :
f(x)= 4x/x²+1
Il faut mettre des parenthèses autour du dénominateur...
f(x)= 4x/(x²+1)
2)Le début de ton calcul de la dérivée est correct mais en développant le dénominateur tu commets 2 erreurs :
* l'une est "tactique" ; il ne faut pas dévemopper le dénominateur qui est un carré car son SIGNE est évident sous forme d'un carré ...
* et si tu développes (je redis , ce serait maladroit !!), il faut te rappeler que (a+b) ² N'EST PAS égal à a²+b² mais à a²+2ab+b² (identité remarquable vue en 4 ème 
)
Bonjour à vous deux,
je ne fais que passer!
@ZEDMATen plus de tes remarques , dans l'énoncé le dénominateur est
dans le calcul de la dérivée le dénominateur se transforme en
sur ce je vous laisse
suite (lis d'abord ce qui précède)
f'(x)=4x*(x²+2)-4x*2x/(x²+2)² J'ai remis en vert, les parenthèses manquantes...
f'(x)=4x²-8x²/x^4+4
f'(x)=-4x²/x^4+4
Au final, le dénominateur est FAUX mais le numérateur aussi. Tu sembles faché(e) avec l'usage des parenthèses....
D'accord,
(x²+2)²=(x²)²+2*x²*2+2²
=x^4+4x²+4
=x^4+x^2
=(x^2+1)
Donc : f'(x)=-4x²/(x²+1)
(J'ai vu les identités remarquables en seconde)
Je crois qu'il te faut reprendre complètement ton calcul de la dérivée en tenant compte en plus de la remarque de Pirho (merci à lui).
Pour ce qui est des parenthèses OBLIGATOIRES dans l'écriture en ligne des expressions algébriques, voici un nouvel exemple :
Quand tu écris :
f(x)'=u'*v-u*v'/v²
.
Il faut écrire :
f'=(u'*v-u*v')/v²
NB : Ne pas confondre f' qui est une fonction avec f'(x) qui est la valeur prise par cette fonction (donc un nombre réel).
(x²+2)²=(x²)²+2*x²*2+2² oui si le dénominateur de f est bien x²+2 ??
=x^4+4x²+4 oui mais je t'ai dit qu'il était "stratégiquement " maladroit de faire ce développement.
=x^4+x^2
=(x^2+1) Ces 2 dernières lignes sont injustifiables !!
Donc : f'(x)=-4x²/(x²+1) Il manque le "carré" au dénominateur.... de la dérivée !! et puis dans l'énoncé f a pour dénominateur x²+1 ou x²+2 ??????
f'(x)=(4(x²+1))-(4x*2x)/(x²+1)²
f'(x)=4x²+4-8x²/(x²+1)²
f'(x)=-4x²+4/(x²+2)
Ta dérivée est toujours fausse.
1)Tu n'as pas réglé tes problèmes de parenthèses (voir le numérateur de ta dernière ligne...)
2) Comment justifies-tu le fait que (x²+1)² devient.... x²+2 ?
IMPORTANT: Quelle est l'expression de f(x) dans ton énoncé ?
Sommes nous d'accord avec cette définition de la fonction que tu dois étudier :
avec x²+1 au dénominateur ?
f'(x)=(-4x²+4)/(x²+2)
Je ne sais pas comment on obtient x²+2
Moi non plus je ne sais pas !! car c'est impossible !
Quand on obtient au dénominateur de la dérivée :
(x²+1)², on est très content et on s'arrête là CAR cette expression est un carré... dont le SIGNE est immédiat (un carré est toujours POSITIF ou NUL).
Dans l'étude des variations d'une fonction,
a) on calcule sa dérivée
b) on étudie le SIGNE de cette dérivée
c) on en DÉDUIT le SENS DE VARIATION de la fonction.
Si on développe (x²+1)² qui est de la forme (a+b)², on obtient :
(x²)² +2*x²*1+1² = x4+2x²+1 car 1²=1*1 = 1. Etudier le SIGNE de ce polynôme du 4ème degré => galère alors que le SIGNE de la forme factorisée initiale est immédiat comme déjà dit.
Pour que l'on avance un peu plus vite....
Je pense que tu as compris que la dérivée cherchée est :
Si on écrit cette dérivée "en ligne" (on n'a pas le trait de fraction...), il FAUT OBLIGATOIREMENT mettre des parenthèses autour du numérateur soit
f'(x) = (-4x²+4) / (x²+1)²
NB : si on oublie ces parenthèses, erreur fatale (surtout si on saisit cette expression sur une calculatrice ou dans un calcul sur ordinateur !!), on saisit en fait une AUTRE expression qui est :
Donc le résultat est f'(x) = (-4x²+4) / (x²+1)²
b) x|-3 1 3 4
4x²+4| + 0 -
(x²+1)²| + 0 +
f'(x) |
L'intervalle est [−3; 3] , quand x va s'annuler pour 4x²+4 ?
Je ne sais pas comment faire pour la suite
Donc le résultat est f'(x) = (-4x²+4) / (x²+1)² OUI
b) x|-3 1 3 4
4x²+4| + 0 -
(x²+1)²| + 0 +
f'(x) |
L'intervalle est [−3; 3] , quand x va s'annuler pour 4x²+4 ?
Je ne sais pas comment faire pour la suite
Pourquoi -4x²+4 devient-il 4x²+4 ?
suite (lis d'abord ce qui précède)
x|-3 1 3 4
(x²+1)²| + 0 +
Que vaut (x²+1)² quand x= 1 ??
Sauf erreur 2² = 4 et pas zéro
suite
La dérivée est un QUOTIENT => pour étudier le SIGNE d'un quotient, on étudie :
* le signe du numérateur (-4x²+4)
fais le
* le signe du dénominateur (x²+1)²
qu'en penses tu ? si tu ne vois pas.... relis les anciens messages 
Le signe du QUOTIENT se déduit des signes du numérateur et du dénominateur... (règle des signes appliquée dans un tableau de signes)
Reprends ton esquisse de tableau après avoir corrigé tes erreurs dans les études du signe du numérateur et du dénominateur.
x |-3 -1 0 1 3
4x²+4| + 0 + 0 +
(x²+1)²| + 0 + 0 +
Tes études de signes sont erronées....
Tu devrais te concentrer un peu plus car tu réitères des erreurs sur lesquelles je t'ai déjà alerté
a) c'est -4x²+4 et ce signe moins change tout...
b) quand x= -1 que vaut (x²+1)² ? sûrement pas zéro .
c)etc...
bonjour,
juste en passant
une remarque sur la saisie dans les messages
on a déja dit (et répété) le coup des parenthèses
mais aussi :
il est impossible (sauf acrobaties) de garantir l'alignement des caractères entre lignes successives !!
ceci donne des messages typographiquement faux.
par exemple ton message dit que pour la valeur -3 le signe est + et que dans l'intervalle ]-3, -1[ on a 0 partout dans cet intervalle !
au minimum il est indispensable de faire Aperçu AVANT de poster, et de corriger tant que l'alignement n'est pas correct
(c'est d'ailleurs pire pour un admin/correcteur car le site supprime les espaces additionnels pour ces gens là)
pour éviter de mélanger quoi correspond à quoi entre les différentes lignes, il est toléré de mettre des tableaux en images
mieux : on écrit en LaTeX avec l'outil d'édition LaTeX de l'ile qui gère presqu "directement" des tableaux de variation
il génère le canevas et on modifie les cases à la place des valeurs d'exemple
et on n'oublie pas de faire Aperçu avant de poster...
D'accord,
J'ai du mal à utiliser le LaTex
x |-3 -1 0 1 3
(-4x²+4)| + 0 +
(x²+1)²| +
Je ne comprends pas
x |-3 -1 0 1 3
-4x²+4| + 0 + 0 +
(x²+1)²| +
Indépendamment de la difficulté (réelle !) de faire des tableaux lisibles dans tes messages
, il y a surtout TES difficultés d'étudier rigoureusement le signe d'une expression comme N(x) = -4x²+4, qui est un banal trinôme du second degré (incomplet) de la forme ax²+bx+c (avec b=0).
Tu as dû étudier en première comment on étudie le signe d'un polynôme du second degré ax²+bx+c selon le signe du coefficient "a" (il y a un théorème bien utile qui résume les différents cas...)
Tu peux utiliser ce théorème avec N(x) = -4x²+4.... pour t'entrainer !! mais ici, il est bien plus rapide (et donc judicieux) d'utiliser la méthode consistant à factoriser -4x²+4...
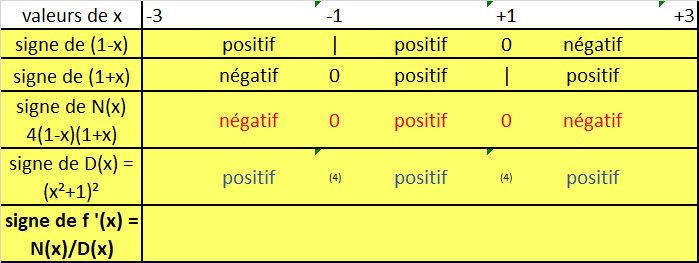
-4x²+4 = 4(-x²+1) = 4(1-x²) = 4(1-x)(1+x) PRODUIT de FACTEURS
En étudiant le signe de chaque facteur de ce PRODUIT de monômes du 1er degré (forme ax +b), on obtient le signe de ce produit
En détaillant l'étude du signe du NUMERATEUR (ce que tu devrais t'imposer de faire plutôt que de multiplier des copier/coller douteux), on obtient :
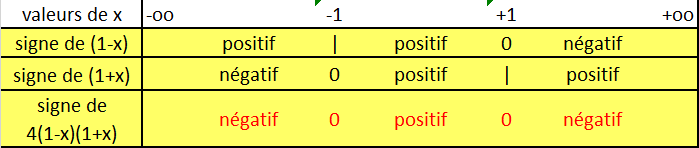
Je vais m'absenter une ou 2 heures.... besoin de prendre l'air 
Finis de remplir le tableau de signes, etc.
d'accord, on ne doit pas remplacer -
et + par -3 et 3 ?Si on connait le signe de N(x) sur IR, on le connait sur [-3;+3].... bien sûr.
C'est ce que j'ai fait dans mon dernier message.
signe de D(x)=(x²+1)²| + 0 + 0 +
NON
Je t'ai déjà fait remarquer que quand x=-1 ou x=1, le dénominateur (x²+1)² vaut.... 4 . Et tu persistes à dire.... zéro , ce qui est faux.
Rappel : Le carré d'un nombre (ou d'une expression numérique) est TOUJOURS positif SAUF si ce nombre est NUL, cas particulier où le carré vaut zéro (car 0² = 0*0 = 0)
Application : Le carré (x²+1)² est toujours POSITIF sauf pour les valeurs de x (si elles existent !!) qui annulent x²+1 (auquel cas on aurait 0*0= 0).
On cherche s'il existe des valeurs de x annulant x²+1...
la réponse est... évidente ! car quel que soit x, x² est supérieur ou égal à 0 donc x²+1 (on ajoute 1 !) est supérieur à 1.
Si pour toi cette évidence, n'est pas... évidente (
), essaye de résoudre l'équation x²+1 = 0 équivalente à x²=-1 : un carré ne peut pas être négatif donc cette équation n'apas de solutions.
Que veut dire les "|" dans votre tableau ?
quelles sont les étapes pour déterminer les signes d'une fonctions ?
Que veut dire les "|" dans votre tableau ?
Ce sont de simples traits verticaux, non indispensables mais qui facilitent la lecture en délimitant bien les "frontières" entre les différents intervalles pour x
quelles sont les étapes pour déterminer les signes d'une fonctions ?
que veux tu dire ?
rappel (c'est du cours BASIQUE
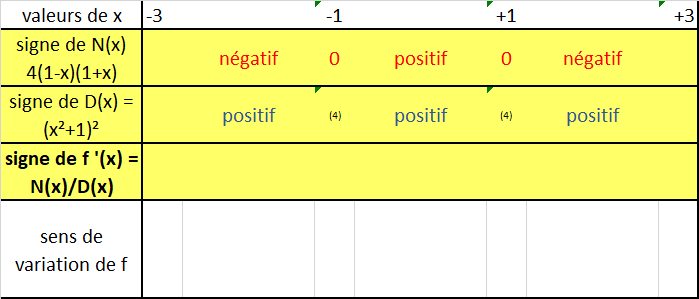
: le SIGNE (positif, négatif, nul sur un intervalle) de f ' , fonction DERIVEE de f, permet de déduire le SENS de VARIATION de la fonction f (croissante, décroissante, constante sur un intervalle)
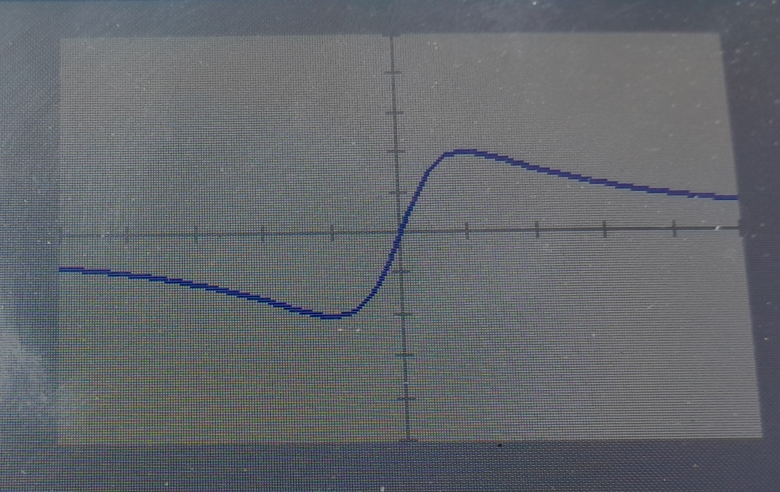
signe de f'(x)=N(x)/D(x) : entre -3 et -1 , la courbe est négatif puis positif entre -1 et 1 et entre 1 et 3 positif
signe de f'(x)=N(x)/D(x) : entre -3 et -1 , la courbe est négatif puis positif entre -1 et 1 et entre 1 et 3 positif
On en était au SIGNE de la dérivée : f '(x) est la valeur prise par la fonction dérivée donc c'est un nombre qui selon la valeur de la variable x peut-être un nombre positif ou un nombre négatif ou un nombre nul.
Je redis ce que tu as dû voir en cours : le SIGNE de la dérivée sur un intervalle de x, permet de savoir si sur cet intervalle la FONCTION f donc la COURBE REPRESENTATIVE de f est croissante, décroissante ou constante (c'est le sens de variation de la fonction).
Dire que la courbe est négatif n'a pas de sens...
Si tu as un logiciel de dessin, fais une copie de mon tableau, complète le puis tu l'enregistres pour ensuite déposer l'image obtenue dans ton message sur le site. Essaye.
Si tu as un smartphone, tu peux faire une photo et l'inclure dans ton message. Essaye.
Tout cela pour t'éviter d'avoir à écrire :
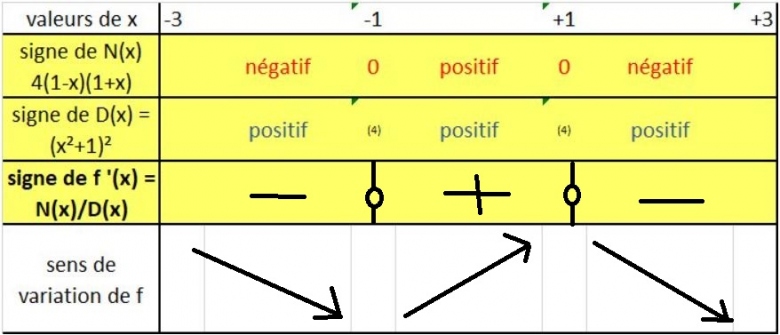
a) quand x appartient à l'intervalle [-3;-1[, alors la dérivée est négative (c'est à dire f '(x) <0).
b) quand x appartient à l'intervalle ]-1;+1[, alors la dérivée est positive (c'est à dire f '(x) >0).
c) quand x appartient à l'intervalle ]+1;3], alors la dérivée est négative (c'est à dire f '(x) <0).
NB : quand x = -1 ou x=+1, f'(x) = 0 (valeurs particulières de x)
Tu avoueras que c'est plus facile à décrire avec un tableau mais le raisonnement reste le même !!
A toi de compléter le tableau avec le sens de variation de la fonction f ou de décrire RIGOUREUSEMENT la situation comme je l'ai fait ci dessus.....
Je vais aller manger 
PAUSE
Super !
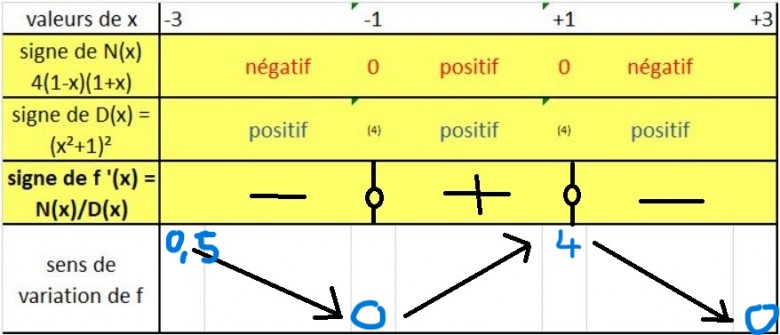
Il ne te reste plus qu'à compléter ce "tableau de variation" avec les valeurs de f(x) correspondant aux valeurs particulières de x... (il y en a quatre).
Tu pourras ainsi répondre facilement à la question c).
Hum !!!
Tu dois avoir oublié des.... parenthèses car tes valeurs sont fausses !
N'as tu pas VERIFIE avec la courbe obtenue ?
suite (lis déjà le précédent message)
Remarque "amicale" :
Il faut que tu comprennes POURQUOI tes valeurs sont FAUSSES.
Déjà en confrontant tes résultats avec la courbe donnée (en 2 minutes !) par ta "super calculatrice" (quelle marque ?), tu aurais dû REAGIR et ne pas fermer tes yeux sur ces valeurs manifestement fausses.
Ensuite, il faut que tu comprennes où est ton erreur car avec ta "supercalculatrice" trouver les valeurs prises par une fonction est...
élémentaire (2 minutes !!). Si ta calculatrice te donne des valeurs fausses (mode table), c'est que tu as commis une erreur en saisissant la fonction (mode graph)...
Je suppose une erreur de parenthèses !! Si tu postes une photo (de l'écran de ta calculatrice), on pourra voir ce qu'il en est.... Tu pourrais aussi poster une photo de la courbe donnée par ta calculatrice, laquelle DOIT bien sûr être cohérente avec le tableau de variation que tu as trouvé en étudiant la fonction...
Comprendre ses erreurs est au moins aussi important que de trouver les bonnes réponses...
Bonjour,
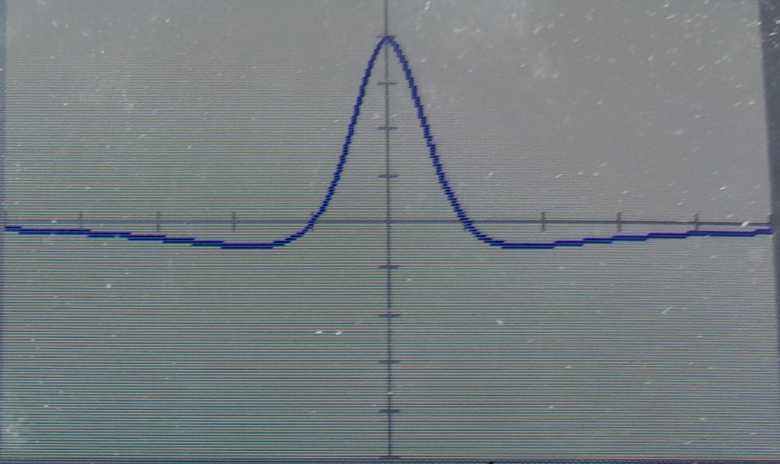
on demande les variations (et donc l'allure de la courbe) de f
pas de sa dérivée !
de toute façon, même avec cette courbe là (celle de la dérivée 
) tes valeurs du tableau de la ligne f étaient "visiblement fausses"
(et pas besoin de calculette pour calculer (de tête !) et
Annuler
connectez vous