Salut
il y a des erreurs dans ta dérivée
<Le a est une constante donc cela fait o
Ensuite tu dérives un produit
Donc tu as u'v+uv' avec u= (x+b) et v=e^-x
la dérivée de x est 1
La dérivée de e^-x est fausse

il te manque un terme la derive de u*v c'est u' *v + v' *u
la derivée de xe^-x= e^-x+e^-x*x*(-1)
voila

Ah oui, j'suis bète (u.v)', il mettait sorti de la tête celui-la...
Merci bien

J'ai une autre question portant sur cette fonction.

Je dois avec le graphique justifié que f(0) = 2 et que f'(0) = 2
A partir de la tangente donnée.

Je vois pas comment à partir d'une tangente je peux justifier ceci.. c'est sûrement bète mais :s

Car je vois bien que la tangente coupe en 2 et que la courbe apparament coupe elle aussi en 2 donc on peut déduire que comme la tangente coupe en 2 la courbe coupe est aussi puisque la tangente est la dérivée de la fonction, ( là je dis sûrement une bétise .. ).

Merci de m'aider à comprendre un peu ceci car à chaque sujet que je vois ça je sais pas quoi mettre, et mon prof les questions comme ça il les passe.

J'ai oublié l'image :s

Bonjour, je ne comprends pas ton graphique. Où est la courbe représentative de la fonction f ?

Bah elle est pas tracée lol, faut répondre à partir de la tangente qu'il y a ... mais moi sans courbe j'y arrive pas non plus

La question est écrite comme ça :
2.a ) En annexe est fourni le tracé de la tangente T à C au point d'abscisse 0.
Ce graphique sera remis complété avec la copie.
Justifier que f(0) = 2 et que f'(0) = 2

C'est pas marqué de la tracé non plus :s

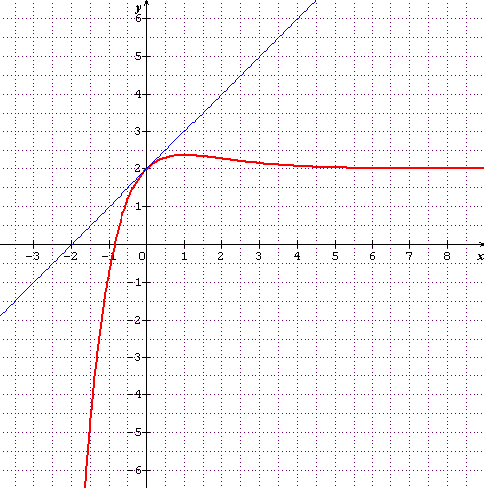
Je te montre à quoi pourrait ressembler ta courbe. Il faut qu'avec les infos que tu as, tu trouves a et b, je suppose, sinon tu ne peux pas la tracer.

Bah de trouber les points a et b c'est la question juste après, donc je pense pas qu'ils demandent de la tracé d'abord et de trouver les points ensuite :s

a et b ne sont pas des points, mais des valeurs.
On ne peut pas justifier que f '(0) = 2 car c'est 1. Vérifie ton énoncé.

Oui je voulais dire des valeurs.
l'équation aves les valeurs a et b : f(x) =

Et j'ai beau lire et relire dans tous les sens c'est bien marqué Justifier f(0) = 2 et f'(0) = 2
Et la tangente passe par ( 0 , 2 ) et ( 1 , 4 ).

Marf j'viens de voir que j'me suis trompé justement sur les coordonnées du second point :s

Alors ton image est fausse ? Pas facile de t'aider si tu postes un mauvais graphique.

Voilà une nouvelle courbe.

Désolé je pensais qu'elle était juste c'est vrai, moi je regardais pas l'image désolé.

Donc ce que j'avais dit plus haut est juste ou non ? :

Je t'ai justifié f(0) = 2

f '(0) = 2 car c'est la pente de la tangente tout simplement : on avance de 1 dans les abcisses et de 2 dans les ordonnées, donc la pente est 2.

D'accord merci bien.