Après j'ai fait = 2x*ln²x+2ln(x)²

Je sais pas du tout si c'est juste

Bonjour...
V(x)=x² (ln(x)²)
V'(x)=2x (ln(x)²)+2 ln(x) x² 1/x
V'(x)=2x(ln(x)²)+2ln(x)x
V'(x)=2x ln(x)(ln(x)+1)

bonsoir

Tu as écrit

V(x)= x²ln²x
V'(x) = u'v+uv'
=2x * ln²x + x²*(2 lnx/x)

Factorise 2 * x * ln x

Bonsoir Agathe-Marie68,

ton expression de la derivee (2x*(lnx)²+x²*(2lnx/x)) est correcte. On peut la factoriser, pour obtenir 2x(1 + Lnx)Lnx. Apres, je crois qu'il faut faire un tableau de  variations avec x, Lnx et 1 + Lnx. On verra alors pour quelles valeurs de x la derivee est negative, positive ou nulle.

Prbebo.

Je vois toujours pas :-S

bonsoir

2x * ln²x + x²*(2 lnx/x)  = 2 * x * lnx * [    +      ]

(lnx)²= 2x*lnx ?
Comme je voi

bonsoir

attention

(lnx)² = ln x * lnx

lns (x²) = 2 lnx

Bonjour a tous,

sur la derivee de V(x) les avis concordent : elle s'ecrit V'(x) = 2x.Lnx.(1 + Lnx). On pouvait aussi l'obtenir en posant g(x) = x.Lnx, soit V = g² et V' = 2.g.g', avec g'(x) = Lnx + 1 (on applique la formule u'v + uv' a la fonction g(x)).

Pour obtenir le signe de variation de V(x), on cherche le signe de V', en etudiant celui de chacun de ses termes :

*   la fonction V est definie pour x > 0 (on peut y ajouter la valeur x = 0 car dans le produit x.Lnx, ou Lnx

Mon ordi m'a joue un tour en postant mon message avant sa fin... je reprends donc :

*   le produit x.Lnx est nul quand x = 0, car si Lnx - quand x 0, c'est la valeur de x qui l'emporte. Je ne sais pas si en terminale on voit les passages a la limite et les formes indeterminees...).

*   La fonction Lnx est negative si x < 1, nulle en x = 1 et > 0 apres.

*   La fonction 1 + Lnx est nulle pour x = 1/e = 0,368, < 0 avant cette valeur, > 0 apres.

On peut donc dresser le tableau suivant :


x                 0                         1/e                             1                                    +
---------------------------------------------------------------------------------------------------

Lnx                        < 0            - 1            < 0              0              > 0                 +

1 + Lnx                   < 0             0            > 0               1             > 0                 +

V'(x)                       > 0             0            < 0               0             > 0                 +

La fonction V(x) est donc croissante entre x = 0 et x = 0,368, decroissante ensuite jusque x = 1, et de nouveau croissante apres, jusque x + .

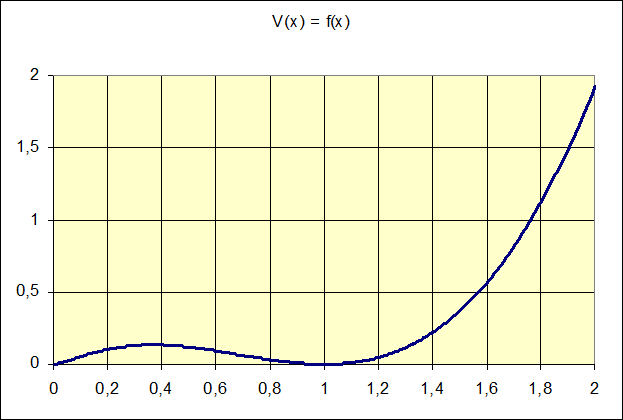
Ci-dessous un trace de V(x) entre x = 0,005 et x = 2.

Prbebo.