Inscription / Connexion Nouveau Sujet
Détermination de la courbe d' une parabole
Bonjour, voici un exercice de mathématiques que j'ai reçu il y a une semaine et que je n'arrive pas à trouver les réponses. Étant en 1ere S, nous étudions en ce moment les paraboles et tout ce qui va avec (forme canonique,etc...)
Voici l' énoncé de l' exercice 
Un architecte réalise le plan d' un bassin dont la forme est représentée ci-contre ( désolé schéma fait avec un logiciel de dessin donc il est mal fait mais on voit l' essentiel )
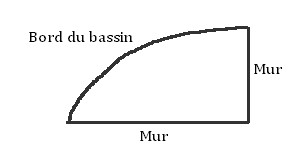
On se propose de définir un procédé géométrique pour construire le bord du bassin
Dans un repère orthonormé :
- on place le point A (-1;0) et un point M (m;0) variable sur l'axe des abscisses avec m appartient à [0;20].
- on construit dans le demi-plan y supérieur ou égale à 0, le demi-cercle C de diamètre [AM] et on note le point K le point d'intersection de C et de l'axe des ordonnées.
- on construit le point B (m,k) où k est l'ordonnée du point K
- enfin on trace la courbe H décrite (je l'appelle comme sa car sur mon énoncé, c' est un signe bizarre) par le point B lorsque m décrit l'intervalle [0;20].
1- Réalisation de la construction
a- Réaliser la construction à l'aide d'un logiciel de géométrie.
b- La courbe obtenue H vous fait-elle penser à une courbe connue ?
2- Détermination de la courbe
a- Déterminer les coordonnées du centre I du demi-cercle C
b- Calculer le rayon de C et en déduire l'ordonnée du point K en fonction de m
c- Quelle fonction f représente la courbe H dans le repère utilisé ?
d- Quel est le sens de la variation de la fonction f sur l'intervalle [0;20] ?
-----------------------------------------------------------------------------------------------------------------
Bon je me suis penché un peu sur cette exercice mais je ne vois vraiment pas comment faire :/
Le petit 1 je l' ai fait, voici la figure :
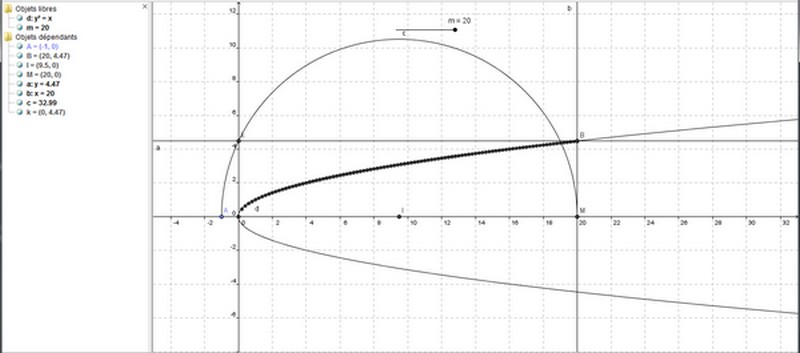
J' ai réussi à trouver l' équation de la parabole qui est une représentation graphique du second degré. Il s'agit de y² = x. Je l' ai trouvé car dans un ancien DM, nous avons x² = y et je m'étais trompé de sens, j'avais inversé les 2 lettres et j'avais trouvé cela.
C' est la 2eme partie qui m'embête, la détermination de la courbe. Je ne trouve pas ce qu'il faut faire. J' ai déjà vu quelques pistes grâce à Géogebra mais sans succès. ( si vous voulez la figure sur Géogebra, demandez-la moi )
Voilà, je vous souhaite de passer une bonne journée.
a)
I milieu de A(-1;0) et M(m;0) car [AM] est un diamètre de C.
donc
b)
[AM] est un diamètre de C donc
Le triangle KOI est rectangle en O donc
donc
…
car k>0
Bonjour Chatof,
Tout d'abord merci de m' avoir répondu.
1- Je voudrais savoir quelle propriété utilisez-vous pour avoir les coordonnées du point I.
Moi j'ai utilisé AM² = ( xa - xm )² + ( ya - ym )² et je trouve AM² = -1 - m² + 0 et vu que AI = IM cela fait I(-1-m²/2;0) et donc nous ne trouvons pas le même résultat
2- Pour trouver le rayon vous faites xm - xa / 2 ? Donc m-(-1) / 2
Ensuite d'où viens le point O et quelle propriété utilisez-vous pour avoir k² + (m-1/2)² ? Vous utilisez k² + i² ?
Désolé de toutes ces questions mais je suis perdu dans ce DM, je n' y arrive vraiment pas et je mélange tout.
Je vous souhaite une bonne après-midi et un joyeux réveillon de Noël.
Bon désolé du double-post mais j'ai trouvé pour le 1 
Il suffit juste de le mettre à la racine en faite vu que c' est AM qu'on cherche et non pas AM² ^^
Par contre pour le 2 je sèche toujours :/
O c'est l'origine du repère O(0;0)
https://www.ilemaths.net/maths_4_pythagore_cours.php
OIK triangle rectangle donc pithagore
IK c'est le rayon du cercle
IK=(m+1)/2
OK = k
OI= (m-1)/2
Merci de m'avoir répondu 
Je vais tâcher de faire Pythagore pour la 2eme question et je vais voir ce que je trouve ^^
Par contre le message suivant correspond à la première question ? Car je galère un peu à comprendre vu qu'on ne trouve pas les mêmes réponses qu'au dessus à ce que j'ai cru comprendre.
Voilà, je vais essayer de résoudre ce problème et je vous tiens au courant.
Joyeux Noël,
Quel livre avez-vous ?
Il me semble que les coordonnées du milieu de 2 points c'est du cours.
« Moi j'ai utilisé AM² = ( xa - xm )² + ( ya - ym )² et je trouve AM² = ( -1 - m )² + 0 »
Donc AM²= (-1-m)²=(m+1)²
donc AM=m+1
donc AI=IM=Rayon=(m+1)/2
donc tout va bien
Donc en résumé pour la question 1, nous faisons AM² = (xa-xm)² + (ya-ym)². On trouve AM² = (-1-m)² + 0 qui équivaut à (m+1)². Donc le rayon est égale à la moitié de cette longueur donc (m+1)/2.
Donc coordonnées de I en abcisse est égale à (-1+m)/2 ou (m+1)/2 ? Car vos réponses sont différentes du début, c' est ca que je ne comprends pas.
Pour le livre, j' ai TransMath 1ere S mais nous n'avons jamais utilisé ce livre. Le prof s'inspire d'exercices et modifient quelques trucs ce qui rend les DM très compliquées.
Ce que je ne comprends pas aussi c'est ca, je ne vois pas c' est pour quelle question :
Joyeux Noël à vous aussi même si il est un peu tard. Bonne soirée 
Ca:
Si I milieu de AB
Alors
en principe c'est du cours
donc on l'utilise pour I milieu de A et M
Donc coordonnées de I en abcisse est égale à (-1+m)/2 ou (m+1)/2 ? Car vos réponses sont différentes du début, c' est ca que je ne comprends pas.
Je ne vois pas ! Où ?
PS: Il est bien votre livre.


