Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Trigonométrie et fonctions trigonométriquesTopics traitant de trigonométrie et fonctions trigonométriques [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Détermination de pi par la méthode d'Archimède

Posté par
Sapphire 28-11-19 à 18:04

Bonjour,
J'ai fait un chapitre sur la trigonométrie en classe pour pouvoir calculer pi avec un cercle trigonométrique et ma prof de maths m'a donné ce sujet là, j'arrive pas du tout à faire la question 2....

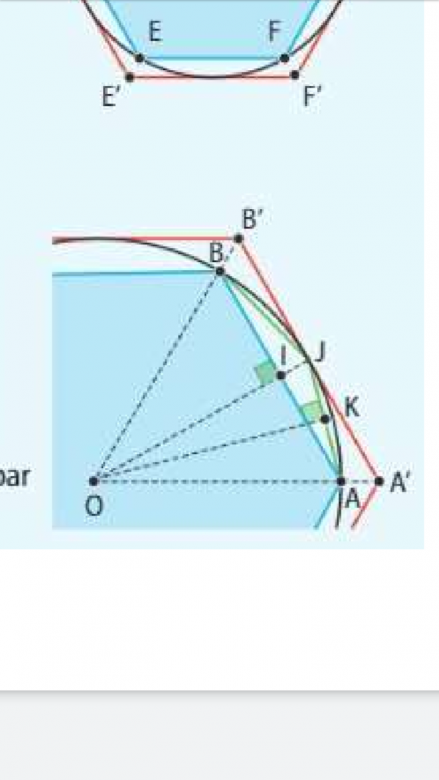
Sur la figure ci-contre, [AB] est un côté de l'hexagone de demi-périmètre Py et [AJ] et [JB] sont des côtés du polynôme inscrit à 12 côtés.
On pose AB= c1'= 1 (je l'ai trouvé dans la première question) et AJ= c2'.
A) Calculer la valeur de OI en fonction de c1' à l'aide du théorème de Pythagore.
B) En déduire la longueur de IJ puis la longueur de AJ en fonction de c1'.
C) en déduire la valeur c2', seconde approximation de pi par cette méthode (j'ai trouvé la première dans la première question)
Merci beaucoup d'avance!

Détermination de pi par la méthode d\'Archimède

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 19:11

Bonsoir

Qu'est-ce qui vous pose problème  ?   Vous connaissez  OA

AB donc AI manque la longueur d'un côté  dans le triangle rectangle OIA

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 19:36

Mais je ne sais pas calculer AI et donc calculer OI

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 19:53

I n'est-il pas le milieu de [AB] ?

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 19:54

Il n'est pas précisé dans l'énoncé

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 20:29

OAB est un triangle isocèle  deux côtés sont des rayons  (OI) perpendiculaire à (AB) donc (OI )  médiatrice

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 20:31

D'aaaaaccord et ça va nous aider à calculer AI grâce à la mesure de l'angle c'est ça?

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 20:59

I est le milieu de [AB]  donc AI=\dfrac{1}{2}AB et comme AB=c_1
On a bien AI

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:04

Donc après on a plus qu'à faire le théorème de Pythagore !

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:16

L'appliquer plutôt

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:17

Oui effectivement 😂

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:19

C'était d'ailleurs indiqué

Posté par
Sapphirere : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:21

Oui je l'avais compris mais je n'arrivais pas à prouver la longueur de AI que j'avais deviné grâce à la figure

Posté par
heklare : Détermination de pi par la méthode d'Archimède 28-11-19 à 22:26

Et on recommence  infiniment par le calcul  difficilement par le dessin


Rechercher
Menu
Espace membre
25 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1724 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !