Inscription / Connexion Nouveau Sujet
Déterminer le centre d'une similitude directe
Bonsoir,
Notre classe de spé vient de commencer les similitudes et j'ai quelques problèmes sur une question,
voici l'énoncé:
Sur la figure di-contre, les droites (AB) et (A'B') sont perpendiculaires et se coupent en O; de plus AB=3 et A'B'=OA=OA'=1.
B'
x
|
|
|
x A'
:
:
:
x-------------x------------------------x
A O B
1.Justifier l'existence d'une unique similitude directe s tranformant A en A' et B en B'
Pour cette question j'ai juste dit que les points A et A' sont distincts et que B et B' le sont aussi et j'en ai conclu que s(A)=A' et s(B)=B'
2.a)Déterminer le rapport de l'angle de s
Pour ça j'ai dit que k =(s(A)s(B))/AB
=A'B'/AB
=1/3
soit /teta = ( vecteur(AB) ; vecteur(A'B') )
= pi/2
b)Soit /omega le centre de s. Construire /omega
C'est Ici que j'ai commencé à ne pas comprendre... je partais de l'hypothèse que O était Omega mais pense que non...
3.On se place dans le repère orthonormal direct(O;vecteur(u),vecteur(v)) où A' a pour affixe i
a.Déterminer l'écriture complexe de s
b.En déduire l'affixe du centre Omega
Bonsoir
angle π/2
==> le centre de la similitude est sur le cercle de diamètre [AA'] et su rle cercle de diamètre [BB']
==> l'intersection des axes convient
Bonsoir Labo
je parlerai même de demis cercles pour lever l'indétermination de la double intersection
illustration
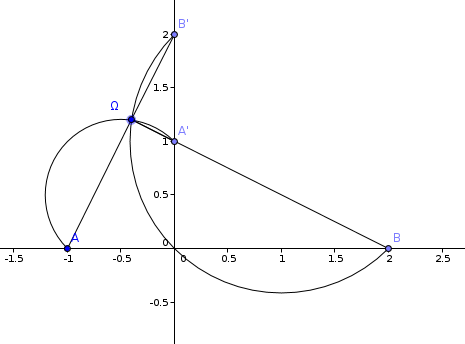
Merci beaucoup =)
pour la 3.a), j'ai dit que l'écriture complexe s'écrivait: z'= (1/3)ei(pi)/2(z-w)+w
et que w=b/(1-a)
mais je sais pas comment trouver w vu que je n'ai pas a et b.
Merci d'avance
je ne sais pas si w=b/(1-a), peut-être. Je ne sais même pas ce que tu désignes par a et b et je n'en ai pas besoin. Mais ce que je sais est que tu as à ta disposition deux points et leur image.
donc, par les affixes des points A ,B ,A' et B'
je trouve a=(1/3)i
donc k = |a|=|(1/3)i|=1/3
comme za'=za+b
b=za'-za
=i+1
donc z'=(1/3)iz+i+1
test
z = -1 (c'est l'affixe du point A)
z' = -1/3i + i + 1 = 1 + 2/3i
or on aurait dû trouver i qui est l'affixe de A', image de A par cette similitude directe.
Same player shoot again
(but with no fault, please)
Je n'arrive pas à comprendre ton raisonnement, aussi je vais te donner le mien, qui est plus basé sur des notions fondamentales et des propriétés essentielles
on sait qu'une similitude directe est une rotation suivie d'une homothétie, les deux pouvant être de même centre, le seul point fixe de la transformation.
une rotation de centre l'origine O du repère, suivie d'une homothétie de même centre se traduit en complexe par une relation de la forme
où est une mesure de l'angle de la rotation
et r 0 est le rapport de l'homothétie.
0 est le rapport de l'homothétie.
si le centre n'est pas O, mais un point d'affixe , cela revient à effectuer une translation du plan, et la formule devient
Ici, on sait que
donc on cherche la transformation qui s'écrit
il reste à déterminer
On sait que le point A d'affixe -1 a pour image le point A' d'affixe i, donc la relation doit être vérifiée entre A et A' (on aurait pu prendre B et B', on se les garde pour une vérification ultérieure)
il reste à résoudre cette équation pour trouver
et on trouve
ce qui nous rassure car le schéma bien fait nous incite à penser que cette valeur est la bonne.
Donc l'application s'écrit
qu'on développe sans faire d'erreurs de calcul, pour trouver finalement
dernière vérification, B a pour affixe 2 et son image B' a pour affixe 2i
est-ce que la relation va le confirmer ?
exact !




