Inscription / Connexion Nouveau Sujet
Déterminer une fonction à partir d'une tangente.
Bonjour,
Je suis totalement bloqué sur ce problème dont voici l'énoncé :
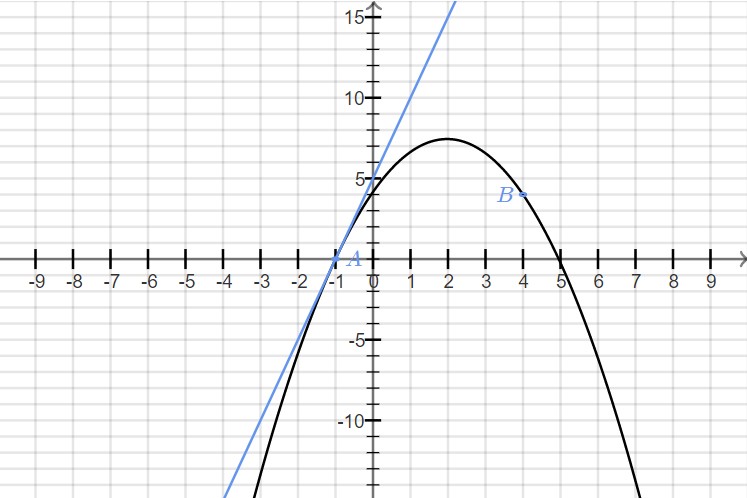
La fonction f représentée par la courbe ci-dessous est de la forme f(x) = ax2 + bx + c.
Cette courbe passe par A (-1;0) et B (4;4) et sa tangente en A est tracée en bleu.
Déterminer graphiquement le coefficient directeur de cette tangente, puis trouver f.
On donnera directement l'expression de f(x)f(x) où aa, bb et cc sont remplacés par leur valeur.
Pour l'instant, je détermine graphiquement le coefficient de la tangente f'(a) = 5.
J'ai essayé de calculer la dérivée de f, soit f'(x) = 2ax + b.
Cependant, je ne vois pas commencer avancer.
Merci d'avance.
Bonjour,
f'(a) = 5 certes, mais c'est quoi "a" ??
certainement pas le coefficient a de "ax²+bx+c" !! faut pas tout appeler "a" !
en quel point a-t-on cette tangente là ?
d'autre part si la courbe de y = f(x) passe par un point de coordonnées (u; v) qu'est ce que ça veut dire ? (de façon totalement générale )
appliquer ça aux points A et B donnés
tu aboutis au final à un système de trois équations à trois inconnues a, b, c
En effet, j'appelle ''a'' le coefficient directeur de la tangente en (-1) même si c'est également le coefficient quadratique de f dans l'énoncé. Par soucis de clarté, je l'appelerai m dans ce cas.
Par ailleurs, si la courbe passe par A et B, je dirais que leurs coordonnées verifient l'équation.
Donc j'obtiens les équations suivantes :
a(-1)² + b(1) + c = 0 
a - b + c =0
a(4)² + b(4) + c = 4 16a + 4b + c =4
En revanche, je ne vois pas de troisième équation ?
la troisième c'est celle avec f'(x)
mais quelle est donc la valeur de m ??
en quel point a-t-on cette tangente là ?
je vois ton problème
avec ta définition de a (ou de m)
le coefficient de la tangente f'(m) = 5.
c'est m = 5
et c'est ausi f'(???)
La valeur de m est -1 dans ce cas.
Puisque la fonction est dérivé en -1 et égale à 5 :
f'(x) = -2a(-1) + b = 5
Ainsi, je trouve le système suivant :
a - b + c =0
16a + 4b + c = 4
-2a + b = 5
En remplaçant c :
c = b - a
16a + 4b + b - a = 4
b = 5 + 2a
En remplaçant b :
c = b - a
16a + 4(5 + 2a) + 5 + 2a - a = 4
b = 5 + 2a
On peux calculer :
c = -62/25
a = -21/25
b = -83/25
On a alors l'équation suivante :
f(x) = 21/25x² + 83/25x + 62/25
Est-ce bien cela ?
Bonjour à tous les deux
AITo, vois cette fiche, lis bien...
Fiche méthode : tracer une tangente à une courbe
et éventuellement celle-ci plus complète : Cours sur les dérivées et la dérivation
équations correctes mais calculs faux.
(sans doute erreurs de signes ou d'additions en reportant la valeur de a dans le calcul de b et c)
de plus tu trouves a = -21/25 (OK celui là)
mais alors pourquoi écris tu f(x) = (+)21/25x² etc ??
Bonjour, malou,
Merci pour les fiches, je vais aller voir.
Et en effet, mes calculs étaient érronés.
Et j'avais renversé tous les signes de la fonctions (il me semble que cela est possible).
Donc cela donne :
a = -21/25
b = 83/25
c = 104/25
Ainsi, f(x) = -21/25x²+83x+104/25
OK
mais erreur de recopie :
f(x) = -21/25 x² + 83/25 x + 104/25
et non une fonction -f(x) n'est pas f(x) !
(la parabole serait retournée verticalement autour de l'axe des abscisses)
c'est pour une équation Expression(x) = 0 que l'on peut multiplier tout par ce qu'on veut non nul (par exemple par -1)
Annuler
connectez vous