Inscription / Connexion Nouveau Sujet
Devoir en math
Salut, j'ai un devoir en math et j'y arrive vraiment pas. Pouvez-vous m'aider svp.
Voici l'énoncé:
On considère la fonction f définie sur l'intervalle]0;+00[ par:
F(x)=-(ln x)2+4ln x-3
Partie A
1a) f' étant la fonction dérivée de f , montrer que f'(x)= (4-2 ln x)÷x
b) En déduire le tableau de variations de la fonction f sur l'intervalle ]0 ; +00[
2)a) Résoudre dans R l'équation x²-4x+3 = 0 et déterminer les abscisses des points d'intersection de la courbe C et de l'axe des abscisses ( vous poserez X = ln x , pour ce dernier point)
b) En déduire par lecture graphique les valeurs de x telle que f(x) > 0
Partie B
Une entreprise constate que la vente de sa production dégage un bénéfice moyen par objet ( en milliers d'euros) égal à :
(ln x)²- 4 ln x+3
ou x désigne le nombre de milliers d'objets fabriqués.
Ce bénéfice moyen par objet n'est pas toujours positif.
1) Calculer le bénéfice total de l'entreprise pour une production de 1 000 objets puis de 3 000 objets.
Indiquer , dans chaque cas si l'entreprise fait un bénéfice positif.
2) Déduire de la partie A pour quelles quantités d'objets l'entreprise fait un bénéfice positif.
Mes réponses :
J'ai commencé à faire quelque recherche et jai trouvé le 1)a) puis pour le 2)a) j'ai fais l'équation et je trouve x1=3 et x2=1, mais je sais pas quoi en faire.
merci d'avance
Bonjour
1 b fait aussi ?
2) comment détermine-t-on les abscisses des points d'intersection de la courbe avec l'axe des abscisses ?
n'oubliez pas de changer votre profil toujours en troisième ?
Alors je sais que la courbe est croissante puis décroissante mais je ne sais pas comment le prouvé avec les logarithmes.
Pour le 2) j'ai vus que c'est un polynome du déco de degrés jai donc calculer le discriminant et jai obtenu, comme résultat final, x1=1 et x2=3 . Sauf que la courbe coupe laxe pour x=2,7 et x=20
Comment on fait pour changer désolé
reprenons dans l'ordre
question 1
calcul de la dérivée d'accord
on sait que
Si pour tout alors
est strictement croissante sur
.
Si pour tout alors la fonction
est strictement décroissante sur
.
donc on étudie le signe de on ne s'occupe pas du dénominateur car strictement positif
vous concluez
question 2 résolution de les solutions sont
et
d'accord
intersection de la courbe avec l'axe des abscisses on résout ou
soit on vous donne une indication
vous poserez X = ln x , pour ce dernier point)
donc que devient cette équation quelles sont les solutions en
dans le rectangle rouge espace membre cliquez sur votre pseudo une nouvelle page s'affiche avec mon compte et en premier mon profil
J'ai toujours pas compris le 1) b)
Justement ça donne X2-4X+3
Donc en x= e1 et x=e3 c'est ça ?
Merci j'ai modifié
Comme l'a bien expliqué hekla, tu cherches à connaître le signe de la fonction dérivée sur l'intervalle
Il t'a donc fait le calcul : f'(x)>0 x<
donc tu fais ton tableau avec comme racine (de l'équation dérivée) e2. tu sais donc pour pour x inférieur à cette valeur, ta dérivée est positive, donc ta fonction croissante, si x est supérieur à cette valeur, alors la dérivée sera négative, et donc la fonction décroissante.
Et oui pour la 2a 
Bonjour, donc e1 et e3 sont la réponses ? Merciii
Donc pour la partie B
J'ai pensé qu'il fallait remplacer x par 1000 oui par 3000. Mais ça m'a l'air faut.. et pour le 2) Je vois pas du tout comment faire..
Ah oui et pour la Partie À 2)a), il faut que je fasse une inéquation avec f(x) ou avec f'(x)
Merci encore pour vos aides
on dit que le bénéfice moyen par objet est définie par
Le texte ne donnant pas de nom au bénéfice moyen je le note et le bénéfice total par
on a alors
le nombre d'objets ou
puisque c'est en milliers d'objets
quelle est votre réponse à la dernière question de la partie A ?
Êtes-vous certaine du texte parce que le bénéfice moyen est défini par
donc on ne peut directement utiliser les résultats de la partie A il faudrait prendre le symétrique de la courbe C par rapport à l'axe des abscisses.
Les valeurs pour lesquelles le bénéfice serait nul ne changent pas mais alors il ne faudrait pas oublier
qu'après objets fabriqués le bénéfice moyen redevient positif
13:10
partie A question 2 a
il n'y a pas d'inéquation à résoudre on vous demande les abscisses des points d'intersection de la courbe avec l'axe des abscisses on résout donc ou
pour ce faire on pose l'équation devient
il n'est pas nécessaire de refaire la résolution de cette équation on connaît déjà les solutions
ou
par conséquent en revenant à on a
ce qui donne
ou d'où
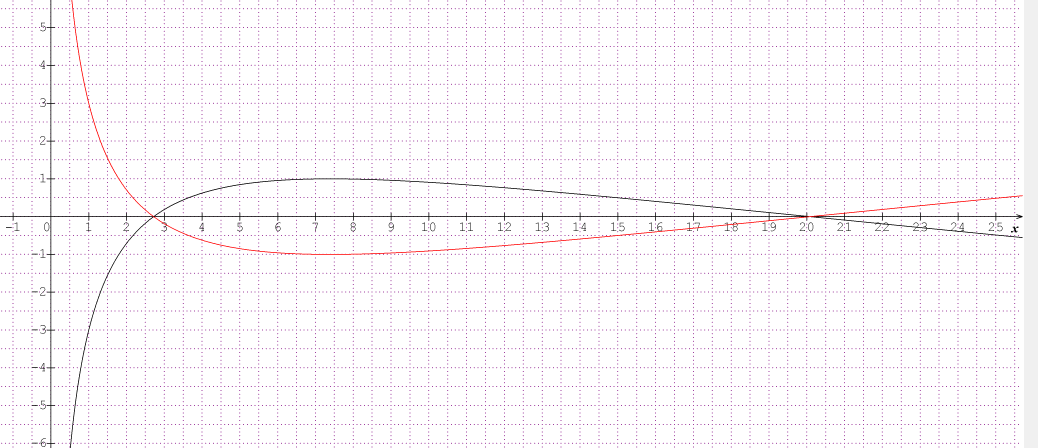
Pour la partie A 2)b) il faut regarder par rapport au graphique et celui nous montre que sur [2.7;20], f(x) >0
Pour partie B 1) jai donc remplacé x par 1 puis par 3 et ça me donne pour x=1 -> 3 et pour x=2 -> -0.187. Et comme on veut le résultat en millier je multiplie le tout par 1000. C'est ça ?
sur
pourquoi 2 on a dit 3000 on veut le bénéfice total on multiplie par le nombre d'objets
il est en milliers d'euros
D'après votre raisonnement le 25/02 à 13h20:
Il faut que je fasse : 1( (ln 1)2-4ln 1+3= 3 et 3( (ln 3)2-4ln 3+3= -0.56. Puis les résultats je les multiplient par 1000 var on les veut en millier
le bénéfice moyen par objet est
où
est en milliers
donc le bénéfice moyen par objet lorsqu'il en vend 1000 est 3
le bénéfice total serait alors de
le bénéfice moyen par objet lorsqu'il en vend 3000 est -0,56
donc pour 3000 le bénéfice serait de
c'est ainsi que je comprends le texte
Je comprend le raisonnement au début car c'est que j'ai trouvé, mais je ne vois pas pourquoi on doit multiplier 3000 et-0.56