Inscription / Connexion Nouveau Sujet
Distance minimale entre un point fixe une courbe
Bonjour à tous, j'ai un exercice à faire pour la rentrée, pouvez-vous m'aidez s'il vous plait?
Merci.
On considère la représentation graphique de la fonction exponentielle dans un repère orthonormé. On cherche ici à répondre à la question suivante: Existe-t-il parmi tous les points de la courbe de la fonction f(x)=ex, un point plus près que tous les autres de l'origine O du repère?
Si ce point existe, déterminer une valeur approchée à 10-2 près de son abscisse et de sa distance au point O.
1) A l'aide d'un logiciel de géométrie dynamique, la tracer la courbe de la fonction exp, créer un point mobile A sur cette courbe, et afficher la distance OA.
En faisant varier A sur la courbe, il semble qu'une valeur minimale de la distance OA se dégage (environ 0,78), pour une abscisse de A environ égale à -0,4.
2) Considérer le point A(x;ex) sur la courbe de exp. Calculer la distance OA, et justifier que l'on cherche à minimiser sur 
la fonction f(x)=e2x+x2. Pour déterminer le signe de f', calculer sa dérivée (notée f'', c'est la dérivée seconde de f).
Dresser le tableau de variation de f' et montrer que f' s'annule une unique fois dans en un réel 
.
Achever en calculant une valeur approchée de à l'aide de la calculatrice, en utilisant le fait que f'()=0
3) On appelle (T) la tangente à la courbe de x
ex au point A(;e)
a) Déterminer le coefficient directeur de (T)
b) Déterminer le coefficient directeur de la droite (OA).
c) Démontrer que les droites (OA) et (T) sont perpendiculaires.
Indication : Avec l'équation f'()=0, on a : e2=-
Merci de votre grande aide
A bientôt.
P.S. : J'ai fait la question 1).
Bonsoir,
Pour la question 2), la distance OA est donnée par OA = 
((xA-xO)2 + (yA-yO)2) = ((x-0)2 + (ex-0)2) = (x2 + e2x). OA sera minimum lorsque x2 + e2x sera minimum (cette dernière expression est bien f(x)).
Cordialement.
Je pense que ca devrait aller tout seul pour la question 3 (elle me semble plus facile) ...Bonjour,
J'ai aussi le même exercice à résoudre pour la rentrée et je n'y arrive pas...
J'ai réussi la première question (très simple) mais la deuxième me pose problème. Je ne comprend pas du tout comment la résoudre.
Serait-il possible, s'il vous plaît, de m'aider ?
D'avance, merci beaucoup de votre aide
Bonjour DTB,
Pour la question 2), la distance OA est donnée par OA = ((xA-xO)2 + (yA-yO)2) = ((x-0)2 + (ex-0)2) = (x2 + e2x). OA sera minimum lorsque x2 + e2x sera minimum (cette dernière expression est bien f(x)). La dérivée est f'(x) = et la dérivée seconde f''(x) =
. La dérivée seconde est strictement positive sur
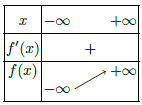
donc f'(x) est strictement croissante sur ce même intervalle. On obtient donc le tableau de variations ci-dessous (il s'agit bien des variations de la fonction f' même si le logiciel l'appelle f). En se basant sur ce tableau et le théorème des valeurs intermédiaires (et son corollaire), on peut affirmer qu'il existe un unique nombre tel que f() = 0. A la calculatrice, on trouve facilement f'(-1) 
-1,7 < 0 et f'(0) = 2 > 0 donc -1 < < 0 (on peut éventuellement donner une approximation avec plus de chiffres après la virgule, l'énoncé ne précisant pas la précision de l'encadrement).
Cordialement.
Merci beaucoup,
Cela me paraît beaucoup plus clair. Juste un petit bémol, je ne comprend pas comment vous avez calculé la distance OA.
Pouvez-vous m'aider ?
La distance OA se calcule par la formule générale de la distance entre deux points. Par exemple, pour A et B: AB = ((xB-xA)2 + (yB-yA)2). Dans le cas particulier de OA, on sait que O(0;0) et A(x;ex), A appartenant à la courbe.
Désolé de vous déranger encore mais l'intitulé que j'ai est un petit peu différent,
La question 2 est la même sauf qu'il est demandé :
Dresser le tableau de variations de f' et montrer que f' s'annule une unique fois dans en un réel ; puis dresser le tableau de variations de f.
Pour finir, identifier le minimum de f et justifier que le point recherché existe, que son abscisse vaut .
Achever en calculant une valeur approchée de à l'aide de la calculatrice, en utilisant le fait que f'()=0
Merci de m'aider svp, je suis perdu là...
Les points supplémentaires sont donc:
a) dresser le tableau de variations de f
b) identifier le minimum de f et justifier que le point recherché existe, que son abscisse vaut ,
les autres points ayant été traités précédemment.
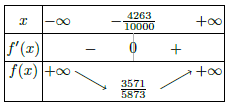
Pour le tableau de variations de f, on sait que f'(x) est négative sur ]-
,] et positive sur [;+[. On en déduit donc le tableau ci-dessous (-4263/10000 correspond à et 3571/5873 à f(), le logiciel ayant fait des approximations car fort logiquement il n'a pas trouvé la valeur exacte de ).
Pour le point b), le tableau de variations montre que f atteint un minimum pour x=. Le point recherché existe donc bien, et sachant que A(x;ex), ses coordonnées sont (;e). Le logiciel nous donne également une approximation un peu plus précise de : -4263/10000 - 0,4263 (qui est bien compatible avec -1 < < 0 que nous avions établi précédemment).
Non, le minimum de f est f() (puisque atteint pour x = ) et le point M (on peut le nommer ainsi) tel que la distance OA soit minimale est M(;e). La distance OM vaudra (f()) soit (2+e2) puisque l'on avait montré que OA = (f(x)).
Bonsoir,
J'ai encore un petit souci en ce qui concerne la dernière question.
Comment prouver que les deux droites sont perpendiculaires ?
Et que trouvez-vous comme valeurs pour les coefficients directeurs ?
D'avance, merci beaucoup
Pour la tangente (T), le coefficient directeur est égal à la dérivée de xex en donc e. Le coefficient directeur de (OA) est (yA-yO)/(xA-xO) soit e/. On sait que deux droites sont perpendiculaires si le produit de leurs coefficients directeurs vaut -1. On peut exploiter cette propriété avec la relation e2=- donnée par l'énoncé pour conclure ...
Bonjour,
J'ai ce même exercice en dm. Je n'arrive pas à démontrer que le coefficient directeur de la tangente T est e
Merci d'avance.
Le coefficient directeur de T en A(;e) est la valeur de la dérivée de xex pour x = . Il faut donc commencer par calculer la dérivée de xex ...
Bonjour,
Merci de me répondre.La dérivée de l'exponentielle c'est elle même. Mais pour obtenir le coefficient directeur de T au point A(; e) on doit appliquer :
y = f'(a) (x-a) + f(a)
y = e (x-)+(e)
Donc e est le coefficient directeur de T ???
Oui, c'est bien cela. On peut effectivement passer par l'équation de la tangente mais on peut aussi directement dire que le coefficient directeur de la tangente est la dérivée au point considéré (soit f'(a) en reprenant ta notation). La dérivée est ex et donc le coefficient directeur e. Tous les chemins mènent à Rome mais certains sont plus directs 
Bonjour a vous tous,
Il se trouve que j'ai moi aussi cet exercice dans un dm mais en plus j'ai une question qui suit la 2 :
Rédiger une solution
A l'aide des deux parties précédentes, rédiger une solution du problème posé.
le problème étant : Existe-t-il, parmi tous les points de la courbe de la fonction x : ->e^x , un point plus près que tout les autres de l'origine O du repère?
Bonne soirée a vous
Manon
Voilà au moins un sujet qui intéresse beaucoup de monde Le problème du point le plus proche de O correspond en fait à la question 2) de l'énoncé initial (où ce point est appelé A). Ce point A existe bien. En effet, la distance OA est donnée par OA = ((xA-xO)2 + (yA-yO)2) = ((x-0)2 + (ex-0)2) = (x2 + e2x). OA sera minimum lorsque x2 + e2x sera minimum (cette dernière expression est bien f(x)). La dérivée est f'(x) = et la dérivée seconde f''(x) =
. La dérivée seconde est strictement positive sur
donc f'(x) est strictement croissante sur ce même intervalle. On obtient donc le tableau de variations ci-dessous (il s'agit bien des variations de la fonction f' même si le logiciel l'appelle f). En se basant sur ce tableau et le théorème des valeurs intermédiaires (et son corollaire), on peut affirmer qu'il existe un unique nombre tel que f() = 0. A la calculatrice, on trouve facilement f'(-1) -1,7 < 0 et f'(0) = 2 > 0 donc -1 < < 0 (on peut éventuellement donner une approximation avec plus de chiffres après la virgule, l'énoncé ne précisant pas la précision de l'encadrement).
Bonjour,
J'ai moi-même cet exercice à faire mais formulé de façon différente:
1. Montrer qu'il existe un unique point A de la courbe C plus près que tous les autres de l'origine O du repère.
2. Déterminer une valeur approchée à 10^-2 près de l'abscisse alpha de A et de la distance OA.
Je ne comprend pas pourquoi il faut étudier la dérivée seconde et comment on arrive à la conclusion qu'il existe un unique point A.
Merci d'avance pour votre aide
Il faut étudier la dérivée seconde pour montrer qu'elle est toujours positive. Ceci permet de dire que la dérivée première est croissante et en calculant ses limites aux bornes, on voit alors qu'elle varie de - à +. La conséquence est alors que la fonction f passe par un minimum unique comme l'indique le théorème des valeurs intermédiaires.
On peut prendre un exemple simple avec f(x) = x2 (parabole). Alors f'(x) = 2x et f''(x) = 2. On voit aisément que f''(x) > 0 sur et donc f'(x) est strictement croissante sur . Étant donné que les limites de f' sont - et + respectivement en - et +, on peut en déduire que f passe par un minimum unique; on retrouve ce résultat graphiquement puisque la représentation de f est une parabole.
Cordialement.
Annuler
connectez vous