Bonjour,
partage les deux bases en 4 et joins les points obtenus.

non justement

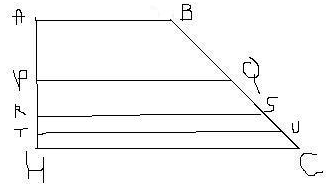
Bonjour, je pense avoir une méthode (que je n'ai pas vérifiée).

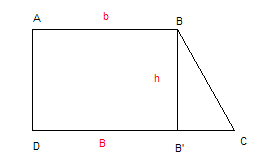
L'aire du trapèze initial est donnée par A=(B+b)h/2 (cf figure ci-dessous) donc l'aire de chacun des trapèzes est donnée par A1=(B+b)h/8.

En notant l'angle BCB', on a tan()=h/(B-b).

Maintenant, notons x1 la hateur du premier trapèze; on commence la construction à partir de la petite base. L'aire de ce premier trapèze s'exprime par la somme des aires d'un rectangle de longueur b et de largeur x1 et celle d'un triangle rectangle de hauteur x1 et de base x1/tan. L'aire du premier trapèze vaut donc A1 = x1.b+(1/2).x1.x1/tan=A/4. A partir de cette équation, on calcule la hauteur du premier trapèze.

Le second trapèze est constitué par un rectangle de longueur b et de largueur x2 (à determiner) ainsi que d'un trapèze de hauteur x2, de petite base x1/tan() et de grande base B2 qu'on peut a priori exprimer en fonction de tan() et de x1 ...

A toi de voir si on arrive à quelquechose avec cela,
++, Matthieu.

salut
suite a mon probleme que je vous ai expose (trapeze rectangle )
j a rrive a ce genre d equation


[((b+B)/2)*H]/4 =   [(b+ (bEA+x)/EA)/2]*x


moi de mon cote j obtiens cela:

-((bx²)/ea) -bx + [((b+B)/2)*H]/4=0

si vous pouviez developper a droite pour que je puisse chercher les racines de cette equation du second degre je vous en remercie davance

*** message déplacé ***

Bonjour,

pourquoi n'as-tu pas poursuivi dans le même sujet

Pookette

*** message déplacé ***

bonjour

une autre méthode avec Thales

tu prolonges le trapèze pour former un triangle : sa hauteur sera H telle que, par Thales :

B/H = b/(H-h) => BH-Bh=bH => H=Bh/(B-b) => H=h/(1-b/B)

après tu prends la prmière hauteur x => cherchons sa base b(x) par Thales

B/H = b(x)/(H-x) => b(x)=B(1-x/H)=B-Bx/H=B-(B-b)x/h

écrivons que la surface avec b(x) vaut le quart du trapèze

(B+b(x))x/2 = (1/4)(B+b)h/2

(B+B-(B-b)x/h)x=(B+b)h/4

2Bhx-(B-b)x²=(B+b)h²/4

(B-b)x²-2Bhx+(B+b)h²/4=0

Delta prime = B²h²-(B-b)(B+b)h²/4 = h²(4B²-B²+b²)/4 = ( hV(3B²+b²)/2 )²

x = ( (B-b)h+/-hV(3B²+b²)/2 )/(B-b) = h(1 +/- V(3B²+b²)/(B-b) ) sous cette forme seule la valeur avec le - convient

x = h(1 - V(3B²+b²)/(B-b) )

Vérifie, j'ai pu faire des erreurs de calculs...

Procède de même pour y et z, les autres tronçons de S/4

Philoux

desole pookette je ne recommencerai plus
merci philoux je vais jeter un oeil a ce que tu viens de proposer
mais j aimerais bien quelqu un confirme mon equation du second degre s il vous plait
il y a juste 2 ou 3 lignes a developper et encore ca prend 2 minutes

"mais j aimerais bien quelqu un confirme mon equation du second degre s il vous plait il y a juste 2 ou 3 lignes a developper et encore ca prend 2 minutes"

rebonjour, qu'est ce que tu appelles 'ea' au juste ?

E est un point qui correspond a l intersection des deux prolongements des cotes du trapeze
le trapeze est donc compris dans un triangle rectangle EHC
ensuite j utilise les triangles semblables EAB EHC
   d ou EA=bH/(B-b)                b=petite base   B=grande base   H=hauteur du trapeze

ensuite
dans EAB  EPQ   EA/(EA+x)=b/PQ   d ou PQ= (b(EA+x))/EA   et x est la hauteur du trapeze ABPQ

je veux  que l aire A(ABHC)/4  = A(ABPQ)

donc ((b+B)/2)*H/4   =  ((b+PQ)/2)*x
en injectant PQ
alors ((b+B)/2)*h/4  =   [(b+(b(EA+x))/EA)/2]*x

je developpe et j obtiens l equation du second degre que je vous ai cite auparavant
merci de confirmer