Inscription / Connexion Nouveau Sujet
DM 1ère S second degré
Bonjour,
Je viens de commencer mon année de 1ère S en me disant que tout sera tranquille jusqu'à ce que je vois le DM que mon prof de maths nous a donné.... Je ne comprend vraiment rien 
Voici l'énoncé :
Dans le livre "la Géométrie " publié en 1637, René Descartes propose une méthode de construction géométrique de la racine d'une équation du second degré. Voici l'extrait du livre et une version plus moderne de la construction.
Extrait du livre
https://www*****
Version plus moderne
https://*****
Questions:
1. a) Réaliser la construction pour résoudre l'équation x²-6x-25=0
b) Calculer la longueur AE
c) Vérifier, en écrivant les calculs, que AE est solution de l'équation
2. Montrer par le calcul que AE est solution de l'équation pour toute valeur positive de p et q
Ce que j'ai fait ( toutes corrections et remarques sont les bienvenues  ) :
) :
1.a)
x²-6x-25
On reconnait ax²+bx-c avec a=1, b= -6 et c= -25
on résout l'équation:
Delta= b²-4ac
Delta= (-6)²-4*1*(-25)
Delta= 36+100
Delta=136
Delta > 0 donc on a 2 solutions:
x1=(-b-racine(Delta)) / 2a
x1=(6-racine(136)) /2
x1=3-racine(34)
x2=(-b+racine(Delta)) / 2a
x2=(6+racine(136)) /2
x2=3+racine(34)
Les deux solutions de l'équation sont 3-racine(34) et 3+racine(34).
b)Avec x²-px-q²=0 et x²-6x-25=0 et AB=q et BC= p/2 , on en déduit que pour ce triangle AB= 5 cm et BC= 6/2=3 cm
Pour calculer AE on utilise le th de Pythagore car le triangle ABC est rectangle en B:
AC²=AB²+CB²
AC²=5²+3²
AC²=25+9
AC²=34
AC= racine(34) cm
sachant que DC, CB et CE sont des rayons du cercle de centre C, on en déduit que DC=CB=CE= 3 cm
AE= AC+ CE
AE=racine(34)+3
AE=3+racine(34) cm
c) Du coup pour le c je sais pas trop parce que j'ai déja écrit les calculs dans le a et le b donc si mes réponses au a et /ou le b ne correspondent pas à la question , dites le moi SVP parce que j'ai l'impression de ne pas avoir utiliser la bonne méthode pour le a.... Ou s'il ya une autre réponse pour le c .
2. QUESTIONS:
Montrer par le calcul que AE est solution de l'équation pour toute valeur positive de p et q.
Je n'ai vraiment pas compris la question et je ne sais pas aussi y répondre...  j'avais peut etre pensé a faire une inéquation mais je ne sais pas comment m'y prendre ni comment la formuler ... HELP !
j'avais peut etre pensé a faire une inéquation mais je ne sais pas comment m'y prendre ni comment la formuler ... HELP !
En vous remerciant d'avance de vos réponses , corrections, remarques et explications que vous pourriez m'apporter .
LOLIPOP02
tu dois recopier l'aide du lien si besoin , et charger la figure correspondante, les extraits de sujet sous forme d'image ne sont pas acceptés...je crois que le contenu du second lien suffira
(modérateur)
Pour ce qui était de la deuxième image je vais juste charger la figure
Voici ce qu'il y avait écrit à coté ( tout ceci est compris dans l'énoncé):
Soit p et q deux nombres positifs et l'équation (E):
x²-px-q²=0
-Construire un triangle ABC rectangle en B avec AB=q et BC=p/2.
-Construire le cercle de centre C passant par B.La droite (AC) coupe le cercle en D et E (E n'appartenant pas à (AC)). La longueur AE est une solution de l'équation (E).
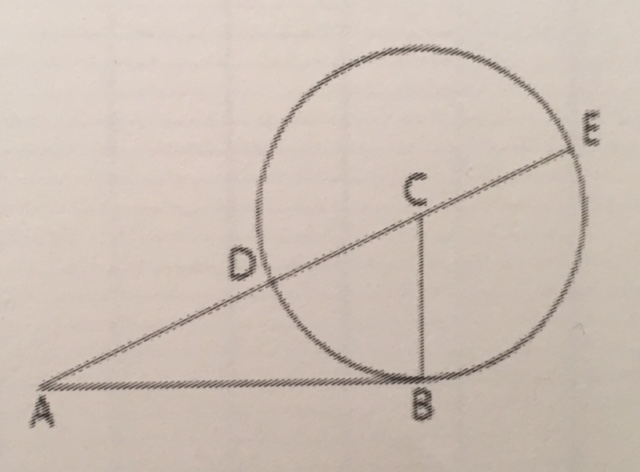
voilà, c'est ce second extrait qui doit te servir pour faire la question 1, et non pas comme tu l'as fait avec le discriminant
Est-ce qu'il faut utiliser la formule x²-px-q²=0 avec x²-6x-25?
Sinon j'ai essayer mais je n'ai pas réussi...
Expliquez-moi SVP 
tu sais lire ? c'est dit ce qu'il faut faire !
Soit p et q deux nombres positifs et l'équation (E):
x²-px-q²=0
-Construire un triangle ABC rectangle en B avec AB=q et BC=p/2.
vu cet énoncé, p ou q peut-il etre négatif ?
mais fais la question 1 !! on ne te demande pas de résoudre l'équation directement !!
1. a) Réaliser la construction pour résoudre l'équation x²-6x-25=0
b) Calculer la longueur AE
c) Vérifier, en écrivant les calculs, que AE est solution de l'équation
Ok j'ai fait réussi à faire le tout le 1 mais je ne comprend pas comment faire le 2... Aidez moi SVP
Pour le b j'ai fait pythagore
Pour le c j'ai fait l'equation x^2-6x-25 en remplacer x par AE c'est à dire 3+racine(34) et j'ai obtenu 0 ce qui veut que AE est solution de l'equation
Qu'en pensez vous ?




