Inscription / Connexion Nouveau Sujet
DM a rendre pr Lundi 15 mars . Sur triangle rect
Bonjour , j'ai un DM a rendre pour Lundi 15 Mars , et je bloque sur la derniere question .
La question est Démontré que le triangle ABC est rectangle en B . Mais on ne connait que la longueur BC = 3.3 cm et AC = 6.5 cm .
Auparavant , danc les autre question on c'est que BPMC est un parallelogramme se qui ma permit de trouvé BC = 3.3cm
Aidez moi s'il vous plait . Merci d'avance !
Sur la figure , BPMC est un parallelogramme tel que BP = 5.6 cm et PM = 3.3 cm
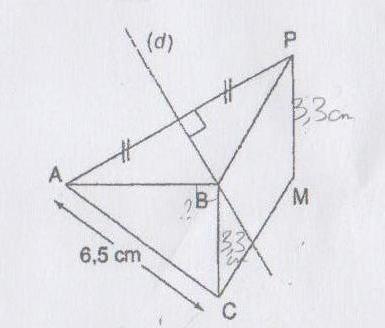
sur la figure on voit dans une meme figure un triangle isocele traversé par une médiatrice ( triangle ABP ), Un parallelogramme BPMC et un triangle ' rectangle ' en B ( triangle ABC )
1°) Démontrer que la droite ( d ) est la médiatrice du segment [ AP ] ( j'ai déja répondu )
2°) Démontrer que le triangle ABC est rectangle . c'est ici que je bloque !
bonjour,
tu sais que ABC est rectangle ?
rectangle en B tu connais AC (hypotenuse), BC un coté de l'angle droit
AC² = BC²+AB²=
6,5²= 3,3²+AB²
AB² = 6,5²-3,3²=
AB² = 42,25-10,89
AB² = 31,36
AB = 5,6
j'ai fait ca d'apres ce que tu ecrit, j'ai pas verifier l'exo en entier
pourrais-tu joindre la figure...
la procédure est ici--->![]() [lien]
[lien]
le point B est sur la médiatrice de [AP] donc AB = BP
et comme BP = 5,6 cm
tu as AB = 5,6 cm
pour démontrer que le triangle ABC est rectangle en B tu peux utiliser la réciproque du théorème de Pythagore puisque tu connais la mesure des trois côtés du triangle ABC...