Inscription / Connexion Nouveau Sujet
DM algorithme
Bonjour à tous !
En essayant de faire mon algorithme j'ai bloqué assez rapidement .
Voici l'énoncé :
Notre personnage est retourné au restaurant d'ou il avait eu tant de mal à rentrer . De nouveau fortement alcoolisé il tente de rentrer chez lui a pied en empruntant un pont sans garde-corps de 15 pas de long et 4 pas de large , sa démarche est très particulière :
-Soit il avance d'un pas en avant
-Soit il se déplace d'un pas en diagonale vers la gauche
-Soit il se déplace d'un pas en diagonale vers la droite
Ces trois déplacements sont aléatoires et équiprobables . On suppose qu'au début de la traversée notre individu se situe au milieu du pont . L'objectif du devoir est de déterminer une estimation de la probabilité de l'évenement R : " L'individu réussit a traverser le pont "
A) Ecrire un algorithme permettant de simuler une traversée du pont. Implémenter le sur une machine ( on munit le pont d'un repère orthonormé O i ,j comme cela : 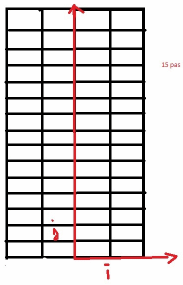 ])
])
Voici mon algorithme et une légende pour mieux comprendre (  )
)
D = Nombre de pas a droite
G = Nombre de pas a gauche
J = nombre de répétion du parcous
I = nombre de pas
R = Nombre de réussite du parcours
p= Aléa
J'ai commencé mon algorithme mais je bloque pour deux raisons :
Je ne sais pas comment je pourrais exprimer en langage mathématiques une analyse a la fin de chaque boucle qui me permettrait de savoir si l'homme ivre est tombé du pont ou pas , je voudrais en effet écrire quelque chose de la sorte ( si plus de deux pas vers la droite ou vers la gauche d'affilé , la boucle est annulé , R=0 )
Ensuite je ne sais pas quelle est la condition pour que l'homme réussisse a traverser le pont , comment avec mes variables exprimer le fait qu'il réussisse le parcours avec mes variables D et G .
Merci de votre aide .
* Océane > image placée sur le serveur de l' , merci d'en faire autant la prochaine fois Nihon
, merci d'en faire autant la prochaine fois Nihon  *
*
Disons que quand P==1 il va tout droit, quand P==-1 il va à gauche en biais et P==+1 à droite en biais.
Quand P==-1, il faut que tu fasses D prend la valeur D+1 mais également G prend la valeur G-1 et
Quand P==+1 ,il faut que tu fasses D prend la valeur D+1 mais également G prend la valeur G+1
Et puis tu ne dois pas mettre un "Pour J allant de 1 à N", tu n'en sais rien le nombre de pas qu'il va faire.
Ta boucle doit être un TantQue D<=15 ET G >-2 et G < 2 Alors
Et en sortie de boucle après le Fin Tantque il faut tester
Si D>=15 alors afficher " je suis arrivé au bout !!!"
Si G < -2 ou G > 2 alors afficher "Haaaaaaaaaaaaaa ....."
ça, ça calcule pour un essai. Pour avoir une statistique pour n essais, il faut englober le tout dans un
"Pour N= 1 to 1000" et comptabiliser dans une variable S le nombre de succès
(remplace le afficher " je suis arrivé au bout !!!" par un S prend la valeur S+1 )
et puis en sortie de boucle calculer S/N, ça te donnera une idée de la probabilité de succès.
C'est vraiment pas bête tout cela, j'ai beaucoup mieux compris maintenant merci beaucoup !
Par contre j'ai encore un petit problème dans mon algorithme , quand je fais le mode pas à pas il y a une erreur a la ligne " P PREND LA VALEUR ALGOBOX ALEA ENT (-1,1) " , je pense que c'est a cause du signe moins non ? Je ne vois pas pourquoi sinon .
Voici un screen de mes algorithmes , juste pour savoir s'il n'y a aucune erreur maintenant ( à part pour l'aléa):
http://www.noelshack.com/2013-44-1383393409-part-b.jpg
http://www.noelshack.com/2013-44-1383393556-partie-2-b.jpg ( Pour le S+0 je ne sais pas s'il était vraiment utile )
Merci , Bonne journée
J'oubliais on me demande d'en déduire un intervalle de confiance pour la probabilité de l'évènement R .
Est-ce que j'ai le droit de choisir n'importe quel intervalle de confiance , comme celui que j'ai etudié en seconde par exemple , l'intervalle de confiance a 95% ?
=> j'appliquerai une loi binomiale de paramètre p = ? , et n = 1000 , l'intervalle de fluctuation a 95% de la fréquence serait [a/1000 ; b/1000] ou a le plus petit entier tel que p(X>=a)>0.025
et b le plus petit entier tel que p(X>=b)>0.0975 ou je trouverai ces valeurs a l'aide d'un tableur . Est-ce une bonne démarche ?
(je n'ai pas réussi a éditer mon message précédent désolé)
Oui met plutôt P PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)
Mais ce qui ne va pas dans ton algorithme c'est que tu réinitialises D et G à 0 dans la boucle TantQue donc tu ne risques pas vraiment de tomber 
Voilà une version qui marche (tu peux la copier/coller mais en mode éditeur de texte dans algobox)
VARIABLES
D EST_DU_TYPE NOMBRE
G EST_DU_TYPE NOMBRE
P EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME
D PREND_LA_VALEUR 0
G PREND_LA_VALEUR 0
TANT_QUE (D<=15 ET G>=-2 ET G<=2) FAIRE
DEBUT_TANT_QUE
P PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)
SI (P==0) ALORS
DEBUT_SI
G PREND_LA_VALEUR G-1
FIN_SI
SI (P==1) ALORS
DEBUT_SI
G PREND_LA_VALEUR G+1
FIN_SI
D PREND_LA_VALEUR D+1
FIN_TANT_QUE
SI (D>=15) ALORS
DEBUT_SI
AFFICHER "Le parcours est réussi !"
FIN_SI
SI (G<-2 OU G>2) ALORS
DEBUT_SI
AFFICHER "Tombé"
FIN_SI
FIN_ALGORITHME
Et pour l'autre :
VARIABLES
D EST_DU_TYPE NOMBRE
G EST_DU_TYPE NOMBRE
P EST_DU_TYPE NOMBRE
N EST_DU_TYPE NOMBRE
X EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME
POUR N ALLANT_DE 1 A 1000
DEBUT_POUR
D PREND_LA_VALEUR 0
G PREND_LA_VALEUR 0
TANT_QUE (D<=15 ET G>=-2 ET G<=2) FAIRE
DEBUT_TANT_QUE
P PREND_LA_VALEUR ALGOBOX_ALEA_ENT(0,2)
SI (P==0) ALORS
DEBUT_SI
G PREND_LA_VALEUR G-1
FIN_SI
SI (P==1) ALORS
DEBUT_SI
G PREND_LA_VALEUR G+1
FIN_SI
D PREND_LA_VALEUR D+1
FIN_TANT_QUE
SI (D>=15) ALORS
DEBUT_SI
X PREND_LA_VALEUR X+1
FIN_SI
FIN_POUR
X PREND_LA_VALEUR X/1000
AFFICHER "Pourcentage de succès :"
AFFICHER X
FIN_ALGORITHME
Merci infiniment c'est très gentil . J'ai bientot finis mon DM , il me reste une question , correspondant encore à un dernier algorithme .
N désigne un entier compris entre 0 et 15 et on note
An l'évènement après n déplacements ,l'individu se trouve sur un point de la droite d'équation x = -2
Bn x =-1
Cn x=0
Dn x=1
En x=2
On note An , Bn , cn , dn et en les probabilités des événements précédents
1) Calculer a0 , b0 , c0 , d0 et e0.
D'après mon énoncé notre individu se situe au milieu de pont donc A0=B0=D0=E0= 0 et C0=1 ( Réponse confirmée par des camarades ( elle sera utile pour la suite)).
2) Montrer que pour tout entier n compris entre 0 et 15
An+1= (an+bn/3)
Bn+1= (an+bn+cn)/3
Cn+1= (bn+cn+dn)/3
Dn+1= (en+dn+cn)/3
En+1= dn+en/3
(j'ai réussi a prouver celà)
C) a l'aide d'un outils informatique , déterminer les valeurs approchées de a15 , b15,c15,d15 et e15.
Déduisez en une valeur approchée de la probabilité que notre individu traverse ce pont.
C'est là que je trouve que mon algorithme est assez ... bizarre !
Merci de votre aide
Quand on parle à algobox, il faut respecter les parenthèses. Exemple
BB PREND_LA_VALEUR (A+B+C)/3
Et puis tu ne fais pas fonctionner la récurrence, il faudrait rajouter dans la boucle des instructions
A PREND_LA_VALEUR AA
B PREND_LA_VALEUR BB
etc ...
Fait marcher N de 1 à 15 (sinon tu joues 16 fois la boucle)
Mais sinon c'est bien, ça devrait donner le résultat.
Oui c'est fait , merci beaucoup , je bloque juste sur la question que j'avais posté précedemment , je ne vois pas comment trouver le a et b :
( Le message de 13h14 :
"J'oubliais on me demande d'en déduire un intervalle de confiance pour la probabilité de l'évènement R .
Est-ce que j'ai le droit de choisir n'importe quel intervalle de confiance , comme celui que j'ai etudié en seconde par exemple , l'intervalle de confiance a 95% ?
=> j'appliquerai une loi binomiale de paramètre p = ? , et n = 1000 , l'intervalle de fluctuation a 95% de la fréquence serait [a/1000 ; b/1000] ou a le plus petit entier tel que p(X>=a)>0.025
et b le plus petit entier tel que p(X>=b)>0.0975 ou je trouverai ces valeurs a l'aide d'un tableur . Est-ce une bonne démarche ? "
Les probabilités elles s'affichent donc tu les as. A+B+C+D+E devrait te donner la probabilité qu'il arrive au bout.
tu as comparé avec ce que l'on obtenait expérimentalement ?
Pour la loi je ne suis pas sûr, pourquoi serait-elle binomiale ?
Ah mais en fait cette question est dans la seconde partie donc on ne peut pas utilise l'algorithme que je viens de faire ,cette question va de paire avec le second algorithme tu avais simulé ,les 1 000 traversées du pont , mais le probleme est que la fréquence de l'évènement R change , mais elle est toujours dans les 0.3XX environ c'est a partir de cela que nous devons en déduire un intervalle de confiance pour la probabilité de l'évenement R . Pour la loi binomiale c'était ma seule idée , je ne savais pas quoi d'autre je pourrais faire c'est pour cela que j'ai proposé ça 
D'ailleurs grâce a toi j'ai vu que j'avais commis une erreur , dans la derniere partie on me demandait de trouver la probabilité que l'individu traverse le pont (avec mon derniere algorithme)et j'avais donc fais A+B+C+D+E mais j'avais divisé par 5 ! Merci encore 



 que je n'avais pas vu
que je n'avais pas vu
