Inscription / Connexion Nouveau Sujet
DM de math
Bonjour, je ne comprend cette partie de mon DM, aidez moi s'il vous plait.
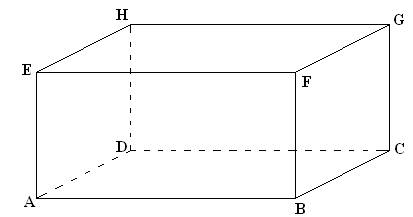
On considère un parallélépipède rectangle ABCDEFGH.
On donne AB=6, BC=4 et AE=3.
I est sur l'arête [BC] et BI = 1,5.
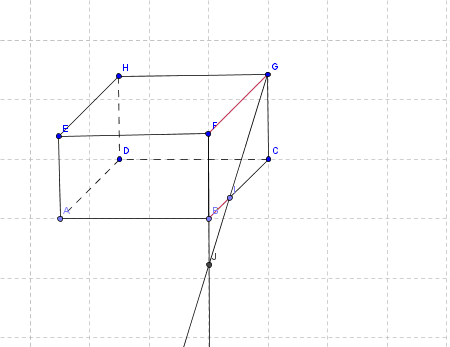
On souhaiterait calculer le volume de la pyramide EGJF dont la hauteur est FJ. On note x=FJ.
a) En raisonnant dans le plan FBC, justifier que x-3/x = 1,5/4
b) En déduire la valeur de x.
c) Calculer alors le volume de la pyramide EGJF.
Merci d'avance
Pour répondre à la première question a) place toi dans le triangle FJG
remarque que (BI)//(FG) et applique Thalès
??
tu écris n'importe quoi, je crois.
quand on écrit les rapports de Thalès, on commence par le point commun aux deux droites. Ici, c'est J.
Ensuite, on vérifie que au numérateur, on a les 3 sommets d'un triangle.. toi, tu as G, I, F, B.. ça ne colle pas.
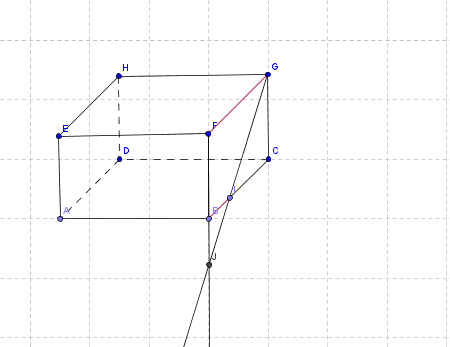
place toi dans le triangle FJG
J, B, F et J,I, G sont alignés dans cet ordre
(BI)//(FG)
tu as un petit triangle : BJI et un grand triangle FJG qui ont un meme sommet : J
vas y !
Pour le grand triangle, c'est JB/JF = JI/JG = BI/FG ?
OUI, c'est juste.
prends JB/JF = BI/FG
et remplace.. tu sais que BI =1,5 FG = 4 JF=x et comment exprimer JB ? à ton avis ?
voyons, toja8113, lis correctement mes posts..
prends JB/JF = BI/FG
et remplace.. tu sais que BI =1,5 FG = 4 JF=x
comment exprimer JB ? JB = JF - BF = x-3
alors, qu'est ce que tu obtiens ?
qu'est ce que tu ne comprends pas pour JB ? Il n'y a rien de spécial à comprendre.
regarde le segment JF, le point B est dessus donc JB + BF = JF
tu sais écrire ça depuis toujours..
donc JB = JF - BF
relis ton énoncé ; on y dit que JF = x et BF = 3
donc JB = x-3
ainsi, JB/JF = BI/FG
==> (x-3)/x = 1.5/4
c'est ce qu'on te demandait de montrer en question a).
Passons à la question b)
à partir de (x-3)/x = 1.5/4 , il faut trouver x..