Bonjour Nazareth060,
pour joindre un schéma et seulement un schéma, pas d'énoncé scanné :

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

Bonjour, je suis bloquer sur mon dm pouvez vous m?aider ?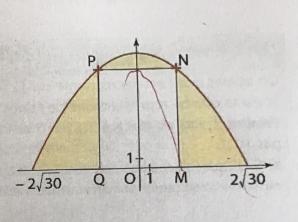



***Image recadrée sur la figure, l'énoncé doit être recopié ! point n°3 de *** Sujet ancien- ne plus donner ce lien-merci

*** message déplacé ***

Bonjour

Il fallait ne copier la figure que sur le sujet que vous avez posté ici Dm de math

Là vous avez fait du multipost

*** message déplacé ***

Bonjour

La fonction est . Vous ne l'avez pas donnée ici

Quel est le problème  ? Vous avez les deux dimensions du rectangle.

Bonjour vraiment désolé c'est la première fois que j'utilise se site. Pour la fonction c'est ça et l'énoncé du problème est :

Déterminer les dimensions de l'ouverture d'aire maximal

C'est donc bien l'aire du rectangle que l'on vous demande.  Vous avez les deux dimensions donc quelle est l'aire du rectangle ?

Désolé mais je n'ai pas d'autre informations

N et P sont des points de la parabole. Quelles sont leurs coordonnées ?

Nous n'avons pas les coordonnées

Il faut utiliser les dérives donc pas de coordonnées

Par exemple si le point G d'abscisse appartient à la parabole d'équation alors ses coordonnées seront

G :  

donc les coordonnées de N et P sont

Monsieur, en toute honnête je n'ai absolument rien compris à ce dm donc je ne serais pas vous répondre

  où est l'ordonnée du point de la courbe d'abscisse  

Un point appartient à une courbe si et seulement si ses coordonnées vérifient l'équation de la courbe.

N a pour abscisse   Par conséquent son ordonnée vaut  

Que vaut MN  ?  Que vaut NP ou MQ ?  

Bonjour.

Tu as la courbe où se trouvent les points N et P.

M et N ont la même abscisse que tu peux appeler x.
Tu connais l'ordonnée de N qui vaut (-0,1x²+12)
Tu connais l'abscisse de Q (et de P) qui vaut (-x)
Tu connais l'ordonnée de Q qui vaut (-0,1x²+12)

Finalement, tu connais les longueurs de MQ (=2x) et de MN (-0,1x²+12)

Donc tu connais l'aire du rectangle MNPQ qui est une fonction de x : F(x)

Il ne te reste qu'à trouver le maximum de F(x) sachant que 0< x <230

A +

Merci infiniment Thierry45mada

Bonjour, Thierry45mada, à la suite de votre réponse j'ai continué mon dm et j'ai fais ceci:

Comme on sait que l'aire d'un rectangle c'est Lxl, on fait (2x ) X (-0,1x^2+12) = -0,2x^3+24x puis on fait la dérivée de cette fonction qui est égal à -0,6x^2+24.

Puis on fait le discriminant qui est positif donc deux solutions, puis j'ai fais mon tableau de variation  et j'ai trouvé les réponses sur l'intervalle ]0 ; 6,32 ].

Pouvez vous me dire si cela est juste ?

Bien cordialement

C'est bien ça.

Il y a deux valeurs de x qui correspondent à des extrema de la fonction F(x).
Tu vois tout de suite que l'une des valeurs n'a aucun intérêt.
Retiens donc l'autre (après avoir vérifié que cette valeur est bien dans le domaine de définition de F) pour terminer.

A +