Inscription / Connexion Nouveau Sujet
DM de maths 2nd
Bonjour j'ai du mal avec mon DM de maths :
Partie A: Sur la figure suivante, M est un point quelconque du segment [BF] de longueur 4 cm.
On a prolongé de part et d'autre ce segment pour construire les points C et D situés respectivement à 1cm de B et de F.
B est le pied de la hauteur issue de A du triangle ACM rectangle en A.
F est le pied de la hauteur issue de E du triangle EDM rectangle en E.
1. En appliquant le théorème de Pythagore dans le triangle ABC et ABM, démontrer que :
AC²+AM²=2AB²+BM²+1
Alors là j'ai trouvé que : le théorème de Pythagore pour ABC est: AC²=AB²+CB²
celui de ABM est : AM²= AB²+BM²
En sachant que CB²=1
On additionne les deux théorèmes est on trouve : AC²+AM²=2AB²+BM²+1
2. On pose BM= x
a. Quel est l'ensemble des valeurs possible pour x ?
b. En appliquant le théorème de Pythagore dans le triangle ACM, démontrer que :
AC²+AM²=x²+2x²+1
3. Déduire des questions précédentes que AB = racine carré de x
4. Justifier que EF = racine carré de 4-x
Merci d'avance .
La figure est comme ça : 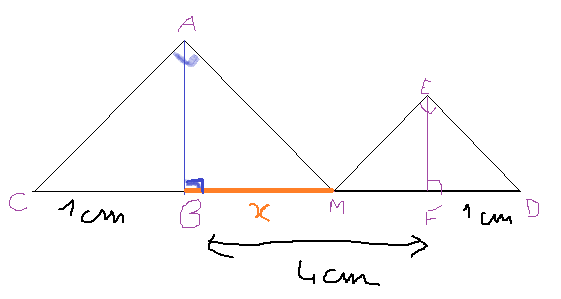
malou > **figure rapatriée***
Bonjour,
2. On pose BM= x
a. Quel est l'ensemble des valeurs possible pour x ?
b. En appliquant le théorème de Pythagore dans le triangle ACM, démontrer que :
AC²+AM²=x²+2x²+1
Merci sbarre
Pour la 2.a j'ai trouvé
0<x<4
Mais pour la 2. b j'ai un problème avec le AC carré et le 2x je n'y arrive pas.
Merci d'avance .
Au fait je me suis trompé dans l'énoncé pour la 2.b l'équation a demontre est:
ACcarre +AMcarre = xcarre +2x +1
Ah oui ok!
Mais du fait qu'il faut utiliser un seul triangle: ACM cela me bloque aussi car dans la question 1 on pouvait additionner Les théorème donc je ne peut pas me servir du triangle ABM. C'est du moins ce que je comprend dans l'énoncé.
Merci
Je ne suis pas sur de comprendre ce que tu as écrit.
Pour la question 1 on te dit d'utiliser Pythagore sur deux triangles parce que l'on a besoin de combiner les deux égalités.
pour la 2 on te demande juste de l'appliquer sur ACM donc une seule égalité basique.
et de nouveau pour la question 3, on va combiner deux égalités (celles trouvées aux questions 1 et 2!)
Si on applique le théorème de pythagorre dans le triangle ACM cela donne:
CM carré = AC carré + AM carré
Donc AC carré + AM carré = CM carré (= x+1)
Il me manque donc des éléments dans mon équation. (x carré et encore 1x car j'en ai déjà un avec CM carré et qu'il m'en faut 2)
Désolé si j'ai du mal à comprendre et encore merci de m'aider!
non (x+1)² ne vaut pas x²+1
identité remarquable à connaitre impérativement!!!
(a+b)² = ... donc (x+1)² = ...
Ah d'accord donc
ACcarre + AM carré = x carré +2x X 1 + 1 carré
= x carré + 2x + 1
Super merci beaucoup!
Et pour la question trois vous m'avez dit qu'il faut faire comme la question 1??
Bonjour j'ai du mal avec mon DM de maths :
Partie A: Sur la figure suivante, M est un point quelconque du segment [BF] de longueur 4 cm.
On a prolongé de part et d'autre ce segment pour construire les points C et D situés respectivement à 1cm de B et de F.
B est le pied de la hauteur issue de A du triangle ACM rectangle en A.
F est le pied de la hauteur issue de E du triangle EDM rectangle en E.
1. En appliquant le théorème de Pythagore dans le triangle ABC et ABM, démontrer que :
AC²+AM²=2AB²+BM²+1
Alors là j'ai trouvé que : le théorème de Pythagore pour ABC est: AC²=AB²+CB²
celui de ABM est : AM²= AB²+BM²
En sachant que CB²=1
On additionne les deux théorèmes est on trouve : AC²+AM²=2AB²+BM²+1
2. On pose BM= x
a. Quel est l'ensemble des valeurs possible pour x ?
Là j'ai trouvé 0<x<4
b. En appliquant le théorème de Pythagore dans le triangle ACM, démontrer que :
AC²+AM²=x²+2x²+1
Là j'ai trouvé qu'il fallait utiliser les identités remarquables:
AC²+AM²= CM²
Avec CM = x+1
AC²+AM²= (x+1)²
AC²+AM² = x² +2x X 1 + 1²
AC²+AM² = x² +2x + 1
3. Déduire des questions précédentes que AB = racine carré de x
4. Justifier que EF = racine carré de 4-x
Merci d'avance .
La figure est comme ça :
https://www.ilemaths.net/img/forum_img/0714/forum_714583_1.png
*** message déplacé ***
Bonjour,
le multi-post n'est pas toléré sur ce site 
tu as certainement oublié de lire ceci en t'inscrivant sur l' :
:
Bonjour j'ai du mal avec mon DM de maths :
Partie A: Sur la figure suivante, M est un point quelconque du segment [BF] de longueur 4 cm.
On a prolongé de part et d'autre ce segment pour construire les points C et D situés respectivement à 1cm de B et de F.
B est le pied de la hauteur issue de A du triangle ACM rectangle en A.
F est le pied de la hauteur issue de E du triangle EDM rectangle en E.
1. En appliquant le théorème de Pythagore dans le triangle ABC et ABM, démontrer que :
AC²+AM²=2AB²+BM²+1
Alors là j'ai trouvé que : le théorème de Pythagore pour ABC est: AC²=AB²+CB²
celui de ABM est : AM²= AB²+BM²
En sachant que CB²=1
On additionne les deux théorèmes est on trouve : AC²+AM²=2AB²+BM²+1
2. On pose BM= x
a. Quel est l'ensemble des valeurs possible pour x ?
Là j'ai trouvé 0<x<4
b. En appliquant le théorème de Pythagore dans le triangle ACM, démontrer que :
AC²+AM²=x²+2x²+1
Là j'ai trouvé qu'il fallait utiliser les identités remarquables:
AC²+AM²= CM²
Avec CM = x+1
AC²+AM²= (x+1)²
AC²+AM² = x² +2x X 1 + 1²
AC²+AM² = x² +2x + 1
3. Déduire des questions précédentes que AB = racine carré de x
4. Justifier que EF = racine carré de 4-x
Merci d'avance .
La figure est comme ça :
https://www.ilemaths.net/img/forum_img/0714/forum_714583_1.png
*** message déplacé ***



