Inscription / Connexion Nouveau Sujet
DM de maths 2nde, valeurs à trouver
Bonjour j'ai un DM à rendre pour demain et moi ainsi que ma classe ne trouvons pas la solution. Voici l'énoncé entier :
Une association humanitaire souhaite creuser un forage qui sera utilisé par trois villages A, B et C. Sur le schéma ci-dessous, les côtés du triangle ABC symbolisent les routes entre les villages.
1) a: Représenter cette situation en prenant 1 cm pour 100m (ce que j'ai fait).
b: Le forage doit être situé à égale distance de chacun des villages (donc je trace les médiatrices pour obtenir un point équidistant des 3 sommets).
2)On note A' (resp.B', resp.C') le projeté orthogonal de F sur la route [BC] (resp. [CA], resp. [AB]).
On note a=FAB' (angle), b=FAC' (angle) et c=FBA' (angle). Donc je note les projetés et je trace les triangles pour trouver les valeurs. Mais c'est précisément là que cela bloque, je n'arrive pas à trouver ces valeurs, j'ai pourtant essayé d'utiliser toutes les propriétés que je connaissais mais ça ne veut pas. Énoncé qui me coince : a: Déterminer les valeurs de a, b et c.
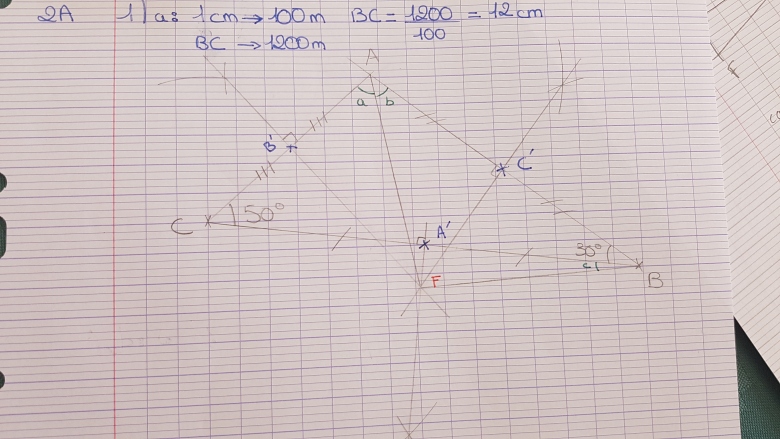
Le rayon est égal à FA=FB=FC dont je ne connais pas les longueurs et je ne peux utiliser la trigonométrie dans les quelques triangles rectangle puisque je n'ai pas de longueurs.
et
interceptent le même arc AC
l'un est un angle au centre l'autre un angle inscrit donc
Dans le triangle AFC isocèle en F, (FB') est médiatrice donc aussi bissectrice donc
Par conséquent comme
donc c=10
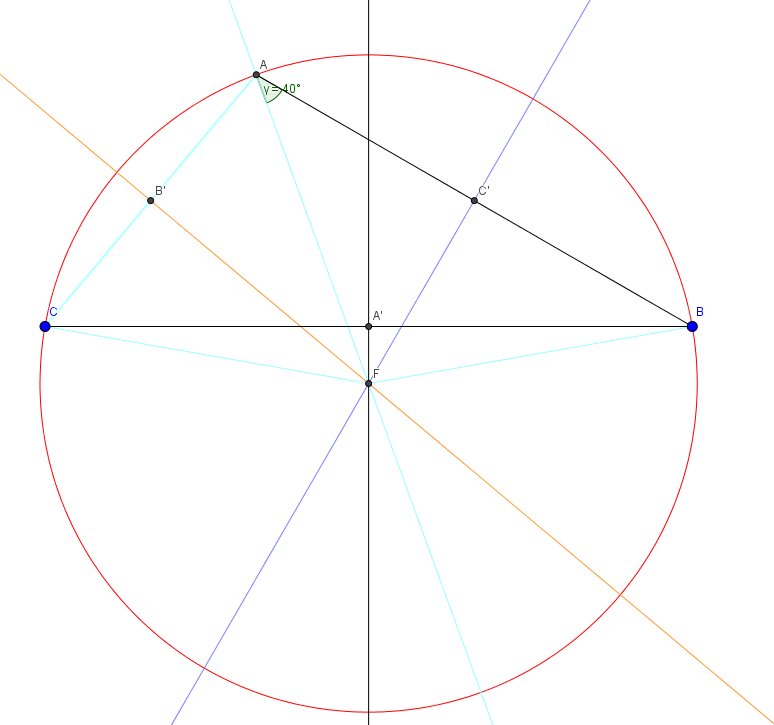
Bonjour j'ai un peu le même sujet mais il y a d'autre questions auxquelles je n'arrive pas à répondre pourriez vous m'aider ?
hekla voici mes questions:
3) a) On note a= PAC, b= PAB et c= PBC
question difficile: déterminée en justifiant les angles a,b,c
question facile qui m'enlève un point au dm: on admet que c=10degres. Déterminer les autres angles b et a en justifiant
3)b) Déterminer la distance du puits a chacun des villages a 1m près.
3)c) Déterminer la distance du puits a chacune des routes à 1m près
Bonjour
Je viens de voir votre message Les valeurs ont été déterminées dans les messages précédents
Qu'est ce qui vous gêne ?
On part des données de la figure
Angle inscrit dans un cercle
les angles et
interceptent le même arc AC
Par conséquent l'angle au centre \widehat{CFA} a pour mesure le double de celle de
donc
On sait que le triangle CFA est isocèle car deux côtés sont des rayons Dans un triangle isocèle les angles à la base sont de même mesure
il reste donc 180-60 à partager en deux donc chacun des angles du triangle CFA valent 60 ce qui en outre montre que le triangle est équilatéral mais ce n'est pas la question.
puisque B' appartient au segment [AC]
\widehat{CAB}=180-(50+30)=100 or \ donc
FAB est aussi un triangle isocèle donc d'où c=10
hekla d'accord il me semble avoir compris je vous en remercie et vous pourriez aussi répondre aux 2 dernières questions que j'ai poser (celle qui ne traite pas les angles) s'il vous plaît ?


