Inscription / Connexion Nouveau Sujet
Dm de maths
Bonjour,
Serait il possible que quelqu'un me fasse un dm de maths qui ce trouve sur ce lien.
***
Merci d'avance à ceux qui répondrons
* Océane > aure2802 si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *
bonjour ,
sur les ordinateurs il y a un clavier et cela est généralement utilise pour écrire ou même recopier des textes.
a plus
Car je suis en semaine de contrôle et je n'ai pas le temps de le faire.
Désoler je n'ai pas recopier le sujet du DM car il est assez long.
bonsoir,
pour A/1 tu as 2 solutions , soit tu prends : et tu developpes en reduisant au meme denominateur et tu retrouveras
soit tu ecris
tu developpes et tu identifies les termes de meme degre
iil existe une troisieme solution : tu effectues la division polynomiale de
par
mais cette solution n'est peut etre pas a ton programme ; c'est la plus rapide
A/2 y=x est asymptote car tend vers 0 pour x tendant vers plus l'infini
re
2b position de la courbe
pour x +
+
donc g(x) est au dessus de l'asymptote .
B/1.
B/2 aire
B/3 aire partie T
aire partie P
voila sauf erreur ; es tu d'accord ????
je suis d'accord avec toi jusqu'à la question B/1. j'ai trouver les même résultats que toi.
Apres pour B/2 Et B/3 je ne comprend pas comment tu fais .
Peux tu m'expliquer comment tu fait pour B/2 B/3
Demain j'essayerai de faire la partie c
Merci Paulo
Si tu as fait la partie C je veux bien voir ce que tu as fait mais moi je la ferai demain ce soir je doit bosser un controle .
re
B/2 c'est l'aire comprise entre la courbe Cg, l'axe des abcisses et la droite x=a
B/3 c'est l'aire calculee dans B/2 moins l'aire du triangle OAB
aire dutriangle OAB
donc aire de B/3 =
Partie C
1/a determiner la derivee de f(x)
et en reduisant au meme denominateur :
1/b signe de f'(x) sur [ 0;+ ]
]
ce serait un peu long de te faire le tableau de variation
la derivee est positive entre 0 et 1 et negative de 1 a plus l'infini
j'ai oublie de te mentionner que la derivee s'annulait pour x=0 et x=1
je te mettrai la courbe apres
la fonction est donc croissante de 0 a 1 et decroissante de 1 a plus l'infini
1/c limite de f en +
tu as du apprendre que dans la recherche des limites la puissace l'emporte sur le
logarithme
pour x +
+
ln(x^2+1) est equivalent a ln(x^2)=2lnx
donc si x  +
+
f(x) est eqivalent a
et si x  +
+
f(x) -
-
la courbe f(x) est la partie rouge en annexe
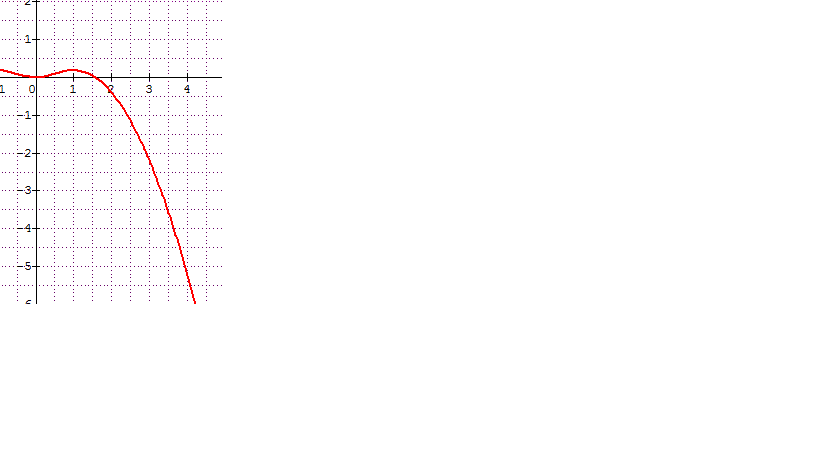
re
pour l'encadrement ,  je l'ai recherche avec un calculateur que j'ai sur mon ordinateur , il faut que tu en fasses autant avec ta calculatice . Je te donne ma valeur que tu peux deviner grossierement avec la courbe en annexe du precedent message
je l'ai recherche avec un calculateur que j'ai sur mon ordinateur , il faut que tu en fasses autant avec ta calculatice . Je te donne ma valeur que tu peux deviner grossierement avec la courbe en annexe du precedent message
j'ai trouve 1,585< <1,586
<1,586
2/b ln(1,58²+1)=1,58²/2
1,251 = 1,248
si tu arrondis au 1/100 : 1,25=1,25
pour 2/c tu te referes a B/3
voila si tu as des questions je regarderai le site demain soir
re
je te joins le tableau du calculateur qui te montre que entre x=1,5852 et x=1,5853 f(x) passe de positif a negatif
bonsoir



