Inscription / Connexion Nouveau Sujet
DM equations différentielles part2
Deuxième partie du DM :
On note f(t)le nombre de ménages vivant en France équipés d'un ordinateur (t est exprimé en années et f(t) en millions de ménages).
On pose t=0 en 1980 et on sait que f(0)=0.01.
Le modèle de Verhulst estime que sur la période 1980-2020, f est solution de l'équation différentielle:
(E1) : y' = 0.022y(20-y) 
0.44y - 0.022y²
1) On pose u= 1/f
Démontrer que f est solution de (E1) si, et seulement si, u est solution de l'équation différentielle :
(E2) : y' = -0.44y + 0.022
--> Alors la j'ai fait u=1/f donc u'=f'/f².
J'ai d'abord transofrmé (E2) : -f'/f² = -0.44 x 1/f + 0.022
f'/f² = 0.44/f - 0.022
f' = 0.44f²/f - 0.022f²
f' = 0.44f - 0.022f²
Donc u est solution de (E2) ssi f est solution de (E1)
2) Résoudre l'équation (E2) et en déduire l'ensemble des solutions de l'équation (E1).
---> Bloqué :'(
3) Démontrer alors que la fonction f est définie sur [0;+[ par :
f(t) 20 / 1+1999e^-0.44t
4)a) Démontrer que pour tout réel t de [0;+[, 0<f(t)<20.
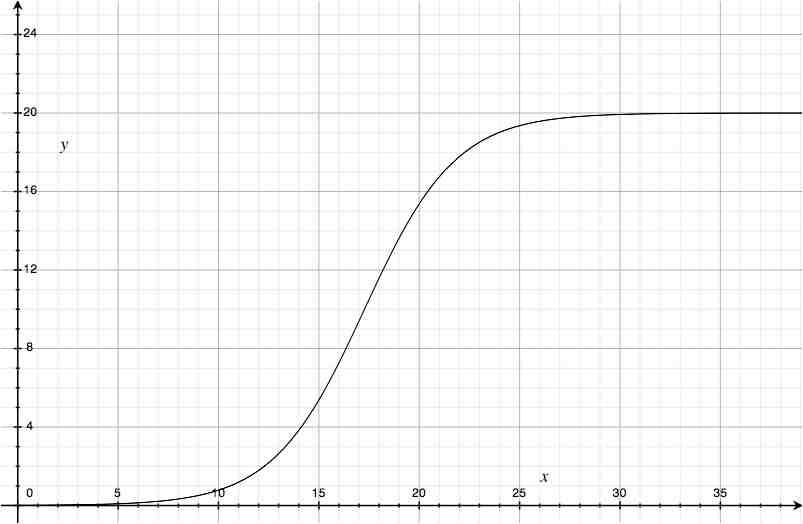
b) Construire la courbe représentative de f dans un repère orthogonal sur l'intervalle [0;40].
Merci de votre aide!
Hello,
2)
Il faut d'abord résoudre l'équation homogène dont les solutions sont :
.
Ensuite il faut trouver une solution particulière de comme par exemple une fonction constante :
On trouve ...et on ajoute les deux types de solutions :
.
ce sont les solutions de (E2).
Tout d'abord merci de ta reponse 
Alors, j'ai bien compris ce que tu as fait mais dans mon cours on applique directement la formule ke^-0,44t - b/a pour avoir l'ensemble des solutions, et ca me donne bien ke^-0,44 + 0,05 = ke^-0,44t + 1/20
Ce sont les solutions de (E2), et d'après 1), u est solution de (E2), donc les solutions de (E1) sont de la forme 1/u car u=1/f .
Les solutions de (E1) sont donc 1/(ke^-0,44t + 1/20).
3) On a donc f=1/u = 1/(ke^-0,44t + 1/20) avec f(0)=0,01
Donc 1/(ke^-0,44t + 1/20) = 0,01
20/20ke^-0,44t + 1 = 0,01
20 = 0,2K + 0,01
(20-0,01)/ 0,2 = K
99,95 = K
Donc f= 20/20x99,95e^-0,44t +1 = 20/1999e^-0,44t
4) euh alors la... Aucune idée...
Arf, je viens de m'apercevoir qu'il me manque 2questions que je n'avais pas vu :
Apres la 4)a), la 4)b) est en fait :
En deduire sans calcul que f est strictement croissante sur [0,+infini[.
Je dois dire que si l'exp' est strictement croissante, alors 1999exp^-0,44t est strictement croissant, etc?
5)a) Calculer la limite de f(t) lorsque t tend vers +infini
Vu la courbe jdirais que ca tend vers 20, mais pour le calcul.. 
5)b) c'etait la courbe, ca c'est bon
4) b)
sans calcul 
Moi je ferais :
comme f(t) est solution de l'équation (E1), .
Or donc
ce qui fait que
, et
est croissante.
5)a)
tend vers 0 donc
tend vers 1 et
tend vers 20/1=20.
Annuler
connectez vous