Inscription / Connexion Nouveau Sujet
DM factorielles n!
Bonjour, j'ai un devoir maison à faire pour la rentrée. Dedans, il y a un exercice sur les factorielles, qui doit nous introduire le cours. Petit problème: n'ayant pas encore fait le cours, je n'y comprend strictement rien !! Voici l'exercice:
Exercice 1:
1- On rappelle que pour n appartenant à IN, il y a n! = n X (n-1) X 3 X 2 X 1 façons de ranger n objets. Soit p un entier inferieur à n. Simplifier si c'est possible:
(n!)^2 n! x p! n! / (n-1)! n! / p! n! + p!
Pour n! / (n-1)! , j'ai trouver que ça vaux n. Et pour n! / p! , j'ai trouvé que ça vaux n x (n-1) x (n-2)... jusqu'à p, mais je ne sais pas comment on l'écrit. Et pour les autres, je ne sais pas si on peut les simplifier. Je pense que (n!)^2 et n! x p! , c'est possible, mais je ne sais pas comment faire.
2- Combien y a-t-il d'arrivées possibles du quinté s'il y a 22 chevaux au départ ? S'il y en a n ?
J'ai trouvé 22^5 donc 5 153 632 possibilités. Et donc s'il y en a n, je pense que c'est n^5. Es-ce bien ça ??
3- Dans une classe de 22 élèves on sélectionne 5 élèves pour un jeu de culture générale. Combien y a-t-il d'équipes possibles ??
La réponse est la même que celle du dessus ?? 5 153 632 équipes possibles ??
Merci vraiment de m'aider, j'ai beau chercher, je ne trouve que ça.
Merci d'avance !!
Pour ton exercice 1 , à part n!/(n-1)! =n et n!/p! = n*(n-1)*(n-2)*...(p+1)...
Je ne vois pas ce que l'on peut simplifier !!!.
Pour le 2.
Combien de posibilités pour la première place ? pour la deuxième ???etc...
Pour la 2ème, je ne vois toujours pas comment faire...
Pour la 3ème, j'ai trouvé (22!)/((22-5)!5!)= 26334, grâce à la formule:
Mais le problème, c'est que vu qu'on a pas encore fait le cours, je ne suis pas censée connaître cette formule. Y a t'il un autre moyen pour arriver au résultat final ?
Merci !!
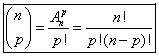
22 x 21 x 20 x 19 x 18 = 3 160 080 possibilités c'est ça ??
Et pour la troisième, c'est la bonne réponse ??
2) Non, avec ton calcul, tu supposes que le premier cheval peut aussi être deuxième...
Ici, on recherche A : les arrivées possibles c'est-à-dire l'ensemble des combinaisons de 5 chevaux parmi 22.
cardA = (5 parmi 22) = 26 334
Et s'il y en a n, ça fera donc (5 parmi n).
3) De même, on recherche B : l'ensemble des combinaisons de 5 élèves parmi 22.
cardB = (5 parmi 22) = 26 334
Si quelqu'un peut confirmer...
Bonjour tout le monde !!
C'est bon, on a eu la correction de ce devoir maison. J'vous recopie la correction, si un de vous en a besoin un jour, ça peut toujours servir !!!
Dans tout les cas, merci beaucoup à Boum2010 et Nofutur2 !!!!
CORRECTION:
Exercice 1:
1) n!/(n-1)!= n
n!/p!= n X (n-1) X ... X (p+1)
2) Le nombre d'arrivées est 22 x 21 x 20 x 19 x 18= 22!/17!=3 160 080.
Pour n, n!/(n-5)!
3) 22!/17! avec ordre donc 22!/(17!x5!)= 26 334 équipes, car toutes les équipes peuvent être ordonnées 5! fois.


