Inscription / Connexion Nouveau Sujet
dm maths
Bonjour, j'ai un DM de mathématiques a rendre demain et je bloque sur le dernier exercice, voici l'énoncé :"ABCD est un carré. On construit à l'extérieur du carré ABCD les triangles équilatéraux BCE et CDF. Quelle est la nature du triangle AEF ? ". En dessinant la figure j'arrive à un triangle équilatéral cependant comment l'expliquer ? Cela va faire un bon moment que je suis sur ce sujet et je ne trouve pas. Ecrivez moi si vous avez une idée, merci beaucoup.
malou > ***au moins la 3e fois que ce sujet passe aujourd'hui...tu as du retard par rapport aux autres ! ***
considère le repère A,B, D
A(0;0)
B(1;0)
D(0;1)
il est facile de démontrer que les coordonnées de E sont (1+( 3)/2);1/2)
3)/2);1/2)
que les coordonnées de F sont (1/2;(1+( 3)/2))
3)/2))
reste à calculer les distances AE,EF et AF et conclure
Bonjour,
comme on laisse le choix des armes
plus simple (= niveau 4ème je pense, au pire 3ème) :
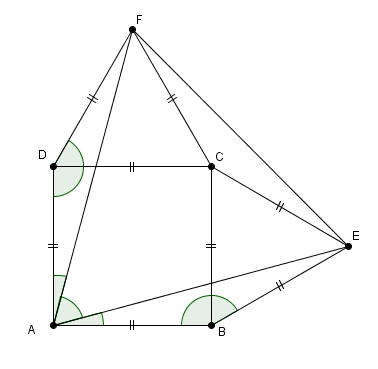
calculer les angles ADF et ABE
les angles ADF et ABE égaux prouvent que les triangles sont ... et aussi ...
en déduire les angles DAF et BAE puis donc l'angle EAF et donc la nature de AEF
si justement, ils viennent d'y rentrer à nouveau, ainsi que les triangles semblables, qui avaient disparu depuis très très longtemps
copie du programme officiel cycle 4 (applicable depuis cette rentrée 2016)
Triangle : somme des angles, inégalité
triangulaire, cas d'égalité des triangles,
triangles semblables, hauteurs, rapports
trigonométriques dans le triangle rectangle
(sinus, cosinus, tangente)



