Bonsoir
tu nous postes la figure que tu as faites ?
à quoi rencontres-tu des difficultés ?

(Notre prof nous a dit de noter que l'aire bleue donc l'aire du quadrilatère = 90/100 x aire marron l'aire du rectangle)

Pour le coup, j'ai du mal avec la question 1: "déterminer l'aire du quadrilatère en fonction de X"

Dois-je d'abord multiplier AB et AD, ou y'a t-il une formule pour déterminer l'aire en fonction de X?

Nous n'avons pas eu de leçon avec ce devoir maison donc je suis un peu paumé pour le coup..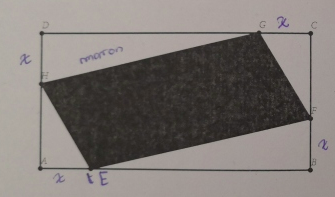


***image recadrée***

Ou bien, AD x AB = 6 donc:
6 x 90/100 = 5,4

l'aire de ton quadrilatère (noir) est égale à l'aire de ton rectangle auquel tu enlèves l'aire des 4 coins
à toi....

Mais du coup, comme je sais que l'aire du quadrilatère = 5,4 (6x90/100) dois-je calculer les 4 triangles ? J'ai un peu de mal avec la question à vrai dire.. Je sais pas si il faut simplement que je m'arrête à 5,4 qui est le résultat de l'air du rectangle x 90/100.

C'est le "en fonction de x" qui me pose problème je pense.

quand tu vas calculer l'aire des 4 triangles, tu vas avoir des résultats en fonction de x
cela veut dire qu'il va y avoir des x dans le résultat

et ensuite, tu feras "aire du rectangle " - "aire des 4 triangles" et donc il y aura aussi des x dans ce résultat

ne fais pas la question 2 avant la 1 (tu ne pourras pas ! )

(Juste avant que le prof nous donne ce devoir maison, on a fait un cours sur les inéquations du 2nd degré mais je ne vois pas le rapport avec ce DM c'est pour cela que je suis complètement perdu.)

Par rapport aux triangles je n'ai aucune idée de comment calculer leur aire. Il n'y a pas de point E sur la figure, comment suis-je censé calculer l'aire des 4 triangles étant donné que je n'ai pas ce point.

Ensuite, je ne sais pas si il faut que divise par 3, et 2 pour trouver les côtés de chaque triangle. Mais du coup, il est dit que AB = x dans l'énoncé donc je ne peux pas diviser par 2. Et puis logiquement je ne connais que AD = 3.

Je n'ai pas la méthode du coup il m'est difficile de procéder au calcul..

bizarre la manière dont tu as mis tes points
AD=3 et AB=2
tu aurais pu mettre tes points pour respecter que AD était la plus grande dimension du rectangle
mais bon, ça changera rien

si AB=2 et AE=x que vaut EB ?
mets toutes tes dimensions sur ton dessin

tu as appris au collège à calculer l'aire d'un triangle rectangle ! ça n'a pas changé

Du coup soit si on prend le triangle EB BF:

EB = 1 (AB = 2, donc 2/2)
BF = 1,5 (AD = 3, donc 3/2)

A = b x h / 2
A = 1,5 x 1 / 2 = 0,75 ?

Et ce, pour tous les autres triangles ?
Je pense que le résultera sera le même pour tous les triangles puisque ce sont les même valeurs à chaque fois.. Éclairez-moi si j'ai faux quelque part !

Le résultat* Désolé pour la faute

non, mais E n'est pas le milieu de...
si AB=2 et AE=x que vaut EB ?

AB = 2 et AE = x donc, EB = 2-x ?

Donc j'ai trouvé:

EBF et HDG = X(2-X)/2
GCF et EAH = X(3-X)/2

Aire de ABCD = 3x2 = 6, donc:

6-[2Xx(2-X)/2] + [2Xx(3-X)/2] ?

bon, ok, tu as compris
utilise * pour multiplier, pour ne pas confondre avec la variable x

de plus, si tu dois prendre le double d'une quantité divisée par 2, il y a quand même plus simple que ce que tu as écrit

aire du quadrilatère = 6-[x*(2-x) + x*(3-x)]

on est d'accord
tu peux simplifier cette expression maintenant

6-[x*(2-x)+x*(3-x)]
6-[-x2+2x-x2+3x]
2x2-6x+6 ?

erreur de développement, fais attention à tes distributivités
touche X² pour mettre au carré avec le 2 entre les balises qui vont s'écrire

J'ai trouvé:

6-[x*(2-x)+x*(3-x)]
2*x²-5*x+6
= 2x² - 5x + 6 ?

exact !
soit A= 2x² - 5x + 6

Parfait du coup j'ai la question 1, merci !
Cependant, j'ai un petit problème avec la compréhension de la question 2..

Dois-je simplement placer le point E sur la figure ?

Enfin j'ai placé le point E de façon logique mais je ne sais pas comment me débrouiller pour la suite..

non, tu dois résoudre cela par le calcul
en utilisant la question 1, et ton 5,4 trouvé hier

Alors:

Je sais que quadrilatère (de la question 1) = 2x² - 5x + 6

Aire noire = 5,4 (6*90/100)

Par quel calcul dois-je procéder?

relis ton énoncé français, et exprime cela par une équation
te la donner n'a pas d'intérêt

On a fait un cours sur les équations du 2nd degré en classe, est-ce en rapport avec cette question 2 ? Je n'ai aucune idée de comment procéder à une équation avec 2x²-5x+6 et 5,4..

De l'aide ?

traduis en math cette phrase

Aire du quadrilatère EFGH (= à 5,4) est égale à 90% de l'aire du rectangle (aire du rectangle = 6)

Soit EFGH = ABCD * 90/100 ?

Je m'embrouille totalement là..

Ou sinon: 2x²5x+6=5,4

D'accord donc:

2x²-5x+6 = 5,4

a = 2
b = -5
c = 6

(b)² - 4ac

(-5)² - 4 * 2 * 6
25 + 48 = 73, √73 = 8,5

- b - √ / 2a = -(-5) - 8.5 / 2*2 = - 3,5 / 1 = 3,5

-b + √ / 2a = -(-5) + 8,5 / 2*2 = 13,5 / 1 = 13,5

{13,5 ; 3,5} ?

Petite erreur : c'est -3,5

du coup {-3.5;13,5} je sais pas si c'est bon !

Ah mais du coup je me suis aidé de mon cours. Mais une coup c'est une équation à 1 solution ?

Toujours pas trouvé.. Je suis complètement embrouillé. Résumons:

Aire de EFGH = Aire de ABCD x 90/100

Ensuite j'ai fait: 2x²-5+6 = 5,4.

Et du coup je n'ai aucune idée de comment résoudre pour trouver x..

oh....tu veux une équation du second degré du type ............=0
que peux-tu faire pour t'y ramener ?

Justement je ne sais pas si la question 2 demande à faire une équation.

Je cite: "Où placer le point E pour que l'aire EFGH soit égale à 90% de l'aire du rectangle ABCD.

si
pour la 2, tu dois faire une équation ! arrête de tourner autour du pot ! et quand tu auras la valeur ou les valeurs de x, eh bien tu sauras où le placer, mais pas avant !

Bon. Du coup on est reste d'accord sur le fait que je dois résoudre cette équation.

2x²-5+6 = 5,4

Et donc, jouer sur les identités remarquables ?

Plutôt: 2x²-5x+6 = 5,4.

Du coup je dois faire une équation du second degré à deux solutions ou inversement à 1 solution ?

Parcequ'ici j'ai fait une équation du second degré à 2 solutions:

Justement, je n'ai aucune idée de comment faire pour avoir une équation du type ............ = 0 à partir de 2x²-5x+6 = 5,4.

Possible d'avoir une piste, voir un exemple ? Au fait, oui je lis vos réponses c'est juste que j'ai du mal avec cette équation.

si tu avais
x+5=3
tu fais comment pour obtenir x ?

Je mets les nombres d'un côté et les x de l'autre:

x = 3 - 5 ?

Ensuite je calcul et je trouve x ect.. Donc je dois faire de mettre pour 2x²-5x+6 = 5,4 c'est bien ça ?

De même*