Inscription / Connexion Nouveau Sujet
Dm maths les lunules d'hippocrate
Bonjour, pouvez vous m'aider je n'y arrive vraiment pas, merci.
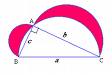
Soit ABC un triangle rectangle en A.
On pose:BC=a,AB=c et AC=b.
E est le demi cercle circonscrit au triangle ABC,E1 er E2 sont les demi-cercles de diametres respectif [AB] et [AC]extérieurs au triangle ABC.Chacun des 2 surfaces sont appelée une lunule.
Démontrer que la somme des aires des 2 lunules est égale à l'aire du triangle ABC.
Merci de me répondre le plus vite possible et encore merci.
Bonjour
Aires lunules = Aire Triangle ABC + 1/2 disque de diamètre AB +1/2 disque de diam AC - 1/2 disque de diam BC
Airres LunuLLes =b*c/2 +1/2( pi*c²/4+pi*b²/4) -1/2(pi*a²/4)=
b*c/2 +1/8pi( b²+c²-a²) = b*c/2 = aire triangle ABC
car a²= b²+c² PYthagore
Bonjour je suis dans la classe de stitch90(coucou!) et j'ai également d'énormes problèmes sur cette exercice et je ne comprends pas votre réponsea ce problème s'il vous plait pouvez vous expliquez en détail?merci
Bonjour,
Il y a 3 demi-cercles
un de diamètre a
un de diamètre b
un de diamètre c
Exprime déjà l'aire de chacun en fonction de a, b, et c
Et puis suis ce qu'a écrit oscar :
L'aire des 2 lunules (ce qui est en rouge) :
l'aire totale (de ce qui est en rouge et en blanc) =====> c-à-d l'aire du triangle ABC + 1/2 disque de diamètre AB +1/2 disque de diamètre AC
et retranche le 1/2 disque de diamètre BC (= tout ce qui est en blanc)
il reste les lunules
oscar a écrit le calcul
est-ce dans le calcul que tu te perds ?


