Inscription / Connexion Nouveau Sujet
DM matrice
Bonjour à tous, j'ai un dm à rendre et je bloque complètement sur la première question. Si quelqu'un pouvait me donner une piste. Merci
Un créateur à fabriqué des sièges ergonomiques à partir de la courbe C représentative de la fonction f définie sur [0;70] par: f(x)= ax^3 + bx² + cx + d où a, b, c et d désignent des nombres réels.
Partie A:
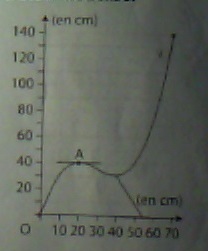
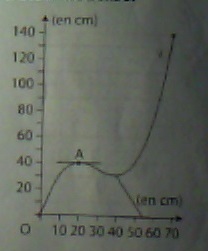
1. à l'aide du graphique expliquer pourquoi d=0 et pourquoi a, b et c sont solutions du système S:
8000a + 400b + 20c = 40
S={ 343000a + 4900b + 70c = 140
1200a + 40b + c = 0
Merci d'avance
bonjour,
Il est facile de démarrer cet exo :
la courbe passe par l'origine ===> f(0)=0 donc d=0
il y a un maximum de coordonnées (20,40) donc f(20)=40 et f'(20)=0
il semblerait que la courbe passe par le point (70,140 ) donc f(70)=140
.......................
la courbe passe par l'origine du repère. quelles sont les coordonnées de l'origine ?
pour x=0 , y=0 soit f(0)=0
en remplaçant x par zéro il reste c=0
Merci, j'ai compris c'est bon.
Mais pour justifier que a, b et c sont solutions du système (S), je ne vois pas trop comment faire le lien entre les points et le système.
bonjour,
Tu as un système de 3 équations a 3 inconnues a, b, et c. Il te faut résoudre ce système. Tu n'as pas d'autre choix .....
Tu peux peut-être uliliser les matrices (puisque c'est le titre de l'exo )
.....................................................
Je ne suis pas sûr qu'il faille résoudre le système, vu que c'est ce qu'on demande deux questions après, avec la calculatrice
Bonjour à tous, j'ai un problème avec mon DM je bloque complètement, j'ai déjà résolu la première partie, c'est avec la deuxième que ça ne va pas.
f est la fonction définie sur [0;70] par:
f(x)= 0,002x³-0,18x²+4,8x
1. Dresser le tableau de variation de la fonction f.
J'ai calculé delta (0.6016), qui est supérieur à 0 donc deux solutions pour f(x)=0 (x1
238,9 et x2-148;9). ces solutions ne sont pas comprises dans l'intervalle [0;70], donc f est strictement croissante sur son intervalle.
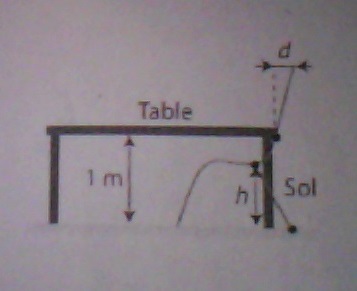
2a. à quelle hauteur h du sol se trouve l'assise du siège ?
AIDE: Au niveau de l'assise, la tangente à la courbe du siège est horizontale.
La je bloque
b. On range le siège sous une table de hauteur 1m. Avec la calculatrice, déterminer une valeur approchée de d à l'unité près.
AIDE: Utiliser la fonction G-Solv ou CALC de la calculatrice.
Merci d'avance.
*** message déplacé ***
Tu as raison . On ne demande pas encore de résoudre ce système mais uniquement de le justifier, ce qui est fait.
Pour la fonction du troisième degré, tu devrais refaire tes calculs . Moi, je trouve les 2 valeurs 20 et 40 correspondant respectivement à un maximum et à un minimum (ce que laisse supposer le graphique ).
.........................
Annuler
connectez vous