Inscription / Connexion Nouveau Sujet
DM : Mesure dans un trapèze.
Bonjour,
Ceci est mon premier post et j'espère ne pas faire d'erreur.
J'ai un DM de mathématiques à rendre pour la rentrée, j'ai résolue 3 des 4 exercices mais le troisième me pose problème, voici l'énoncé :
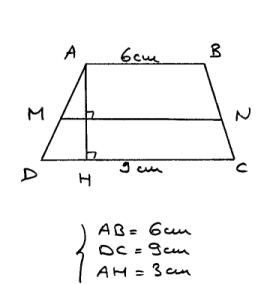
ABCD est un trapèze tel que (AB) est parallèle à (CD).
M et N sont des points des côtés [AD] et [BC] respectivement tels que (MN) est parallèle à (CD).
[AH] est une hauteur de ce trapèze et AH=3cm.
A quelle distance de la base [AB] doit-on tracer la droite (MN) pour que MN=8cm ?
Conseil: on peut considérer le point d'intersection O des droites (AD) et (BC).
Tout d'abord j'ai pensé a utiliser le théorème de Pythagore pour trouver la longueur AD afin d'utiliser en suite le théorème de Thalès mais le problème est que je ne connais pas la longueur DH.
Ensuite j'ai essayé d'utiliser le Théorème de Thalès uniquement mais comme précédemment il me manque une mesure.
Voilà j'espère avoir été clair merci de bien vouloir m'aider (un indice peux me suffire).
bonjour
DH=9-6=3cm
tu calcules en suite AD
tu prends O intersection de (AD) et (BC)
Par Thalès, tu calcules OA
puis par Thalès à nouveau, tu calcules AM
et si tu ne t'en sors pas, reviens
salut
(1) Thalès dans ODC :
OA/OD = 6/9
OA/(OA+AD) = 2/3
... produit en croix...
donc OA = 2AD
(2) Thalès dans OMN :
OA/OM = 6/8
OA/(OA+AM) = 3/4
... produit en croix...
AM = OA/3
AM = 2AD/3
(3) Thalès dans ADH :
AM/AD = d/3
d = 3AM/AD
d = 3(2AD/3)/AD
d = 2
J'ai compris le (3) mais dans le (1) et le (2) je ne comprend pas comment tu passes de :
OA/OD = 6/9
à
OA/(OA+AD) = 2/3
et de :
OA/OM = 6/8
à
OA/(OA+AM) = 3/4
Si je crois avoir compris, ça reviens au même d'écrire :
OA/OD = 6/9
OA/(OA+AD) = 6/9
OA/(OA+AD) = 2/3
Mais après c'est ton produit en croix que je n'arrive pas à voir :
C'est OA=(2(OA+AD))/3 ?
Merci pour ton aide.
C'est bon j'ai réussi le produit en croix, je te tiens au courant pour la suite de l'exercice.
Merci encore.
Juste une question, j'ai bien obtenu d=2, cela veut dire que AM=2.
Je nomme P le point d'intersection entre AH et MN.
J'ai besoins de la distance AP et non de AM.
Chez moi, d n'est pas égal à AM.
d est la distance cherchée entre les droites (AB) et (MN), c'est-à-dire ton AP.
Tu aurais pu t'en rendre compte en regardant plus attentivement les calculs de (3). Mon "d" ne peut être que cela.




