Inscription / Connexion Nouveau Sujet
DM première S Optimisation
Alors voilà j'ai un dm de maths qui est en deux parties, l'une était une conjecture à partir du logiciel géogebra que je pense avoir réussi mais la seconde partie est plus compliquée d'où mon appel à l'aide :
On considère un carré ABCD de côté 1 et M un point mobile sur le segment [AB].
Les droites (DM) et (AC) se coupent en un point E.
On pose AM=x (on a x€[0;1]) et on note H et K les pieds des hauteurs issues de E dans les triangles EAM et ECD.
(a) Démontrer que EH=x/(1+x) et EK=1/(1+x)
Indication : EH+EK=... et EH/EK=...
Merci d'avance 
Bonjour
• une figure permet de mieux voir ce qu'il se passe
la joindre (
[lien] question 5 de la FAQ) au besoin, attention, uniquement des figures
• à part considérer les hauteurs homologues de deux triangles semblables (kesako ??),
il faudra faire deux fois Thalès pour EH/EK
(EH+EK est trivial, lui)
H et K sont indispensables sur cette figure !!
sinon quels Thalès pourrait on bien imaginer qui comporteraient EH/EK si ces points ne figurent même pas sur le schéma ??
Cette figure c'est la feuille que je dois rendre à mon professeur sur la partie 1 où je ne devais pas faire figurer H et K
Merci beaucoup Madame Leile je vais essayer, je vous préviendrai si j'ai réussi ou si j'aurais encore besoin d'aide
je réitère :
applique Thalès pour écrire EH/EK (AM // DC, M, E, D et H, E, K alignés, etc..).
tu peux discuter sur la figure, mais il te faut bien placer les points E et K !
et pour la 3ème fois (4ème ou 5ème peut-être), applique Thalès !
Cette figure c'est la feuille que je dois rendre à mon professeur
cela n'empêche que en pus de cette figure que ti dois rendre il faut bien que tu en aies une de figure avec H et K dessus !!!
ne serait-ce que sur ton brouillon
cadeau :
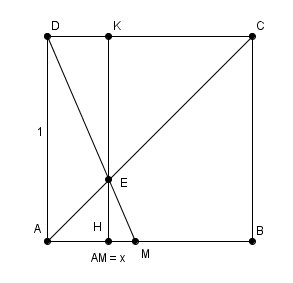
Merci beaucoup Monsieur ça m'a beaucoup aidé
Madame Leile pour l'instant j'ai trouvé :
EA/ED=EM/EC=AM/DC et on sait que AM vaut x et DC vaut 1 donc AM/DC=x/1
Après je ne vois pas trop quand faut-il que j'utilise une seconde et une troisième fois Thales
ni d'ailleurs dans les triangles EAM et EDC
et c'est la combinaison des deux Thalès :
celui avec les triangles EAM et EDC mais écrit correctement !!!
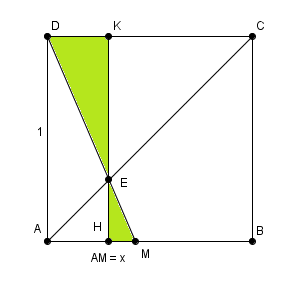
et celui avec EHM et EKD en vert sur ma dernière image) , lui aussi écrit correctement !!
qui donnera la solution
A bon ? Je ne vois pas pourquoi EA/ED=EM/EC=AM/DC ne fonctionne pas, pouvez-vous m'expliquer s'il vous plaît.
Et je suis d'accord avec vous pour votre dernière affirmation mais je ne vois pas pourquoi vous me le dites puisque je ne l'ai pas utiliser 
y a pas de "moins" dans Thalès car ce sont des mesures de longueurs
EM/ED=EH/EK=MH/DK oui
EM/ED=EA/EC=MA/CD=x/1 oui
et en comparant les deux c'est fini
(x/1 s'écrira x bien entendu x ...)
ensuite de
EH + EK = 1
et de EH/EK qu'on vient de calculer
on pourra en tirer EH et EK chacun en fonction de x
(c'est comme un système d'équations à deux inconnues EH et EK, x est supposé "connue" et s'écrit x )
Ce que vous avez mis en rouge c'est juste ou c'est à cooriger ?
Et désolé' d'être pas très compréhensif mais je vois pas comment tirer EH et EK en fonction de x.
ce qui était à corriger c'était la suppression de tous ces signes moins.
c'est fait.
les couleurs c'est juste un indice pour montrer ce qui est égal entre les deux
et donc que tout ça peut s'écrire sous la forme d'une seule longue chaine d'égalités
et celles qui nous intéressent étant celles en vert.
(on ne voit trop le vert à l'affichage sur le site, le bleu n'est guère mieux quand on en met)
donc au final tout ça donne EH/EK = x (on ne garde que ces deux là qui étaient en vert)
ou encore EH = EK*x
à remplacer dans EH+EK =1
et ca donnera EK (en fonction de x) vu qu'il ne reste plus que des EK (et des x) là dedans !
ensuite on trouve EH avec EK*x vu qu'on a maintenant EK en fonction de x
(calculs littéraux élémentaires avec une technique de résolution d'un système de deux équations à deux inconnues EH et EK par la méthode "de substitution", déja mentionné qu'il fallait considérer ça ainsi)
Donc pour EK :
EK+EH=1
EK*1+EK*x=1
On met EK en facteur :
EK*(1+x)=1
EK=1/(1+x)
Puis pour trouver EH:
EH=1-EK
EH=1-(1/(1+x)
EH=(1*(1+x)/(1+x))-1/(1+x)
EH=(1+x-1)/1+x
EH=x/(1+x)
MERCI BEAUCOUP !!!
Bonsoir à tous, j'ai un dm de maths dont je bute sur une question.
On considère un carré ABCD de côté 1 et M un point mobile sur le segment [AB].
Les droites (DM) et (AC) se coupent en un point E.
On pose AM=x (on a x€[0;1]) et on note H et K les pieds des hauteurs issues de E dans les triangles EAM et ECD.
EH=x/(1+x) et EK=1/(1+x)
(a) En déduire qu'une expression de l'aire grisée en fonction de x est :
A(x)=(x^2+1)/2(1+x)
Je ne vois comment procéder pour y arriver !
Merci d'avance !
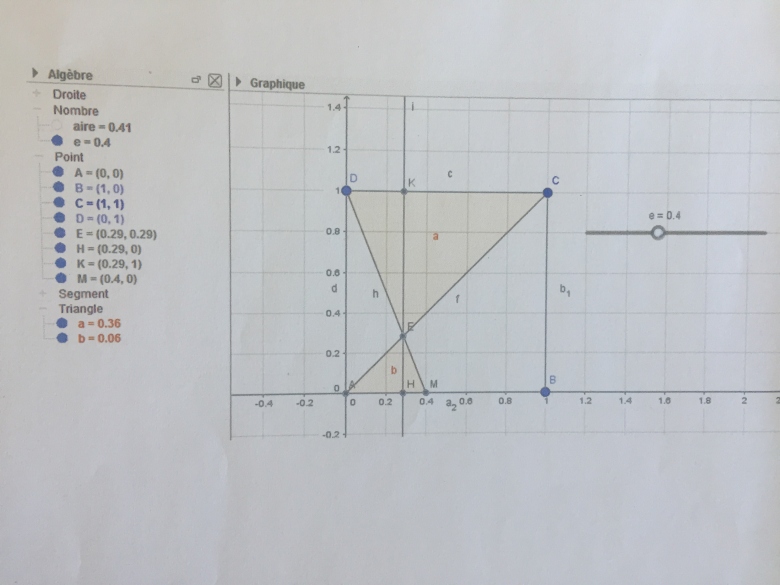
*** message déplacé ***
Bonjour
L'aire grisée est constituée de deux triangles dont on connaît les bases et les hauteurs
*** message déplacé ***
OH nan je viens de remarquer la debilite de la question et sa facilité !
Merci encore
*** message déplacé ***
il fallait rester dans le meme topic ! DM première S Optimisation
*** message déplacé ***
la FAQ du forum
) :
Annuler
connectez vous