Inscription / Connexion Nouveau Sujet
Dm Problème calcul + fonction de
Bonjour je dois rendre un dm pour demain j'ai réussi tous les exercices appart 1, d'ailleurs presque personne de mes potes y arrive. Je vous remercie d'avance de prendre de votre temps pour m'aider.
Enoncer: "ABCD est un quadrilatère dont les diagonales sont perpendiculaires et tel que AB=2017 BC=2018 et CD=2019. Calculer AD et l'exprimez en fonction de x."
bonjour,
en attendant le retour d'Yzz, à qui je rendrai la main :
as tu fais une figure ?
comment peux tu écrire AB et CD en fonction de BC ?
voici une figure :
pour plus de rapidité d'écriture,
tu peux écrire BC = x
exprime AB et CD en fonction de x
j'appelle H le point d'intersection des diagonales.
note HB = a , HA=b, HC = c et HD=d
dans chaque triangle rectangle, applique pythagore pour écrire 4 relations.
vas y !
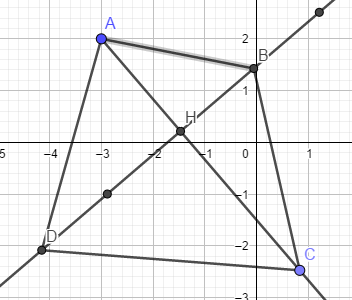
oui mais je ne sais pas du tout si elle est juste. Et vraiment je ne sais pas, j'arrive a faire les en fonction de...
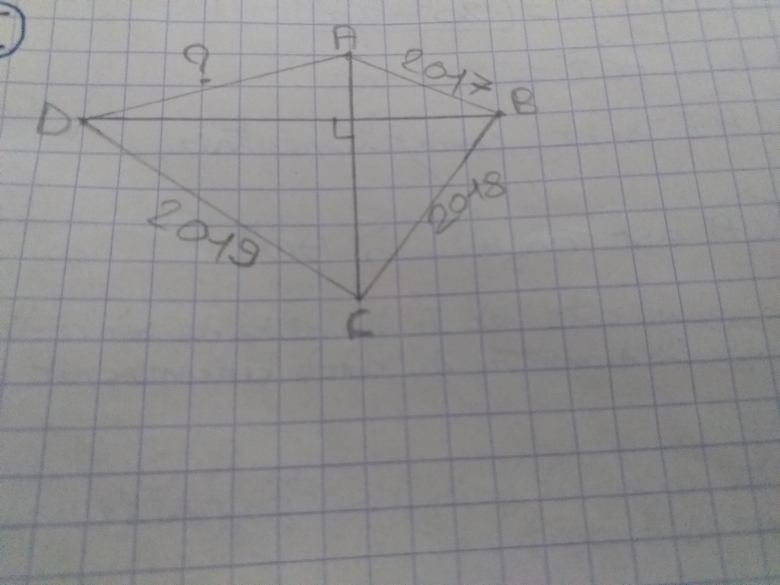
AB²=HA²+HB²
BC²=HB²+HC²
DC²=HC²+HD²
DA²=HD²+HA²
oui, si BC = x, comment écrire AB et CD en fonction de x ?
Okey
Je ne sais pas trop faire mais :
AB²=HA²+HB² DC²=HC²+HD²
AB²=HA²+BC²-HC² DC²=BC²-HB²+HD²
Je sais mettre le x soit BC dans le calcul mais après je ne sais pas comment on peut faire pour faire disparaître les autres.
Es-ce que j'était bien parti déjà ?
Victor365
si BC = 2018 et AB = 2017 tu peux écrire que AB = BC - 1 , n'est ce pas ?
et donc que AB² = (BC-1)² ?
et DC= 2019, donc DC = ??? etc...
avec BC = x
comment s'écrivent tes 4 relations ?
Donc CD=BC+1 alors CD²=(BC+1)².
Et mes 4 relations de bases sont ça:
AB²=HA²+HB² et AB²=(BC-1)² alors HA²+HB²=(BC-1)²
BC²=HB²+HC² BC²=2018² alors HB²+HC²=2018²
DC²=HC²+HD² et DC²=(BC+1)² alors HC²+HD²=(BC+1)²
DA²=HD²+HA² alors DA²=(BC+1)²-HC²+(BC-1)²-HB²
Mais là je me perd un peu, es-ce cela ?
avec BC = x
on a bien
(1) (x-1)² = HA² + HB²
(2) x² = HB² + HC²
(3) (x+1)² = HC² + HD²
et on cherche AD² qui est égal à HA²+ HD²
on va utiliser (1) (2) et (3) pour éliminer HB² et HC² à droite de l'égalité.
effectue (1) - (2) + (3) membre à membre
ça donne :
à toi !
Je ne suis pas sur mais c'est ça ?
On fait:
AD²=HA²+HD²
AD²+BC²=(x-1)²-HB²+(x+1)²-HC²+HB²+HC²
=(x-1)²+(x+1)²
tu n'as pas écrit (1) - (2) + (3) membre à membre, là..
mais je crois qu'on arrive à la même chose..
(1) - (2) + (3) membre à membre donne :
(x-1)² - x² + (x+1)² = HA² + HB² - HB² - HC² + HC² + AD²
(x-1)² - x² + (x+1)² = HA² + AD²
(x-1)² - x² + (x+1)² = AD²
développe et réduit le membre de gauche,
tu auras alors exprimé AD² en fonction de x (donc en fonction de BC).
AD²+BC²=(BC-1)²+(BC+1)²
AD²+BC²=BC²-1+BC²+1
AD²=BC²
euh non ! revois tes identités remarquables :
(a-b)² = ??
(a+b)² = ??
Ah ouiii,
C'est (a+b)²=a²+2ab+b² et (a-b)²=a²-2ab+b²
Mais ducoup le résultat à la fin AD²=BD²+2
AD=BD + Racine carré de 2
C'est ça ?
AD² = BC² + 2
et dire ensuite de AD = BC + 
2, non, ça c'est faux !
AD = (BC² + 2) (et tout est sous la racine !)..
à présent que tu as exprimé AD en fonction de BC, tu peux appliquer aux nombres.
AD² = 2018² + 2 =
trouve AD (et profite en pour remarquer que c'est différent de 2018 + 2 ).
sur ma figure, j'avais pris AB = 3, BC=4 et CD = 5
AD² = 16 +2 ===> AD = 18 = 4,2426
alors que 4+ 2 = 5,1414...
C'est OK pour toi ?
D'accord j'ai compris mais quand on met la racine carré:
AD=Racine carré(BC²+2)
Après ça fait pas 2018+2 en gros c'est la racine carré de 2018²+2 (c'est la racine de tous ça) car on additionne d'abord les 2 vu que la racine carré prend les 2.
On est d'accord ?
AD est presque de même mesure que BC quand les mesures sont grandes, mais si tu as lu mon dernier message attentivement, tu as vu que quand les mesures sont plus petites, la différence entre AD et BC est nette.
Donc tu en peux pas conclure que AD = BC environ. ca dépend de l'application numérique.
et pour revenir sur la racine :
(a + b) n'est pas egal à a +b.
(cf. cours sur les racines).
OK ?
Annuler
connectez vous