Inscription / Connexion Nouveau Sujet
DM sections planes (fonctions d'utilité, courbes d'indifférence)
Bonjour, j'ai un devoir maison en spé math, mais en cours on vient juste de terminer la leçon sur les sections planes, et je n'arrive pas à faire le lien avec ce cour. Pouvez vous m'aider à comprendre cet exercice, sans pour autant le faire à ma place ?
Merci d'avance, Anna.
Un consommateur dispose de deux biens A et B en quantités respectives x et y. A chaque couple (x ,y) de consommations possible, on veut associer un nombre indiquant le degré de satisfaction ou d'utilité du consommateur. On utilise pour cela des fonctions de deux variables appelées fonctions d'utilités. Les courbes de niveau correspondantes sont appelées courbes d'indifférence.
x et y sont les quantités respectives des deux produits A et B. f est la fonction d'utilité qui, au couple (x, y) associe f(x, y) = 5xy.
1. Quelle est la nature des courbes d'indifférence ?
2. Dans un repère orthonormé (O;i;j), représenter la carte des courbes de niveau de f de satisfaction 500, 400, 300, 200 et enfin 100.
3. Le consommateur a une contrainte budgétaire : il ne peut pas dépenser plus de 400 €. Or le produit A est vendu 25 € l'unité et le produit B est vendu 30 € l'unité.
a. Exprimer cette contrainte budgétaire en fonction de x et de y.
b. Tracer la droite d'équation 25x + 30y = 400.
c. Sous la contrainte budgétaire de ce consommateur, peut-on avoir une satisfaction égale à 300 ? à 200 ?
Bonjour annna
Je vois que tu es en rade, là...
Que ne comprends-tu pas ? Le principe des courbes de niveau ou autre chose ...
1) Les courbes d'indifférences (courbes de niveau) ont une équation de la forme , soit de la forme
.
Ce sont donc des hyperboles.
2) Tu représentes les hyperboles d'équations : 5xy=500 ; 5xy=400 ; ....
Ces équations sont équivalentes à .
3a) Il est facile de voir que la contrante est : (à moins que tu ne le voies pas
 )
)
etc...
Bonjour Hiphigenie, merci pour votre réponse, en fait je ne comprenait rien du tout 
Je n'avais jamais fait d'exercices comme ça, sans avoir une équation de surface.
pour la 1) j'ai compris ce qu'il fallait faire, pour la 2) aussi, mais il me semble que vous vous êtes trompé,
car 5xy=500 <=> y=500/5x <=> y=100/x
Maintenant que vous l'écrivez je vois bien ce qu'il fallait faire pour la 3)a), ensuite pour la 3)b) on obtient 25x + 30y = 400 <=> 30y = 400 - 25x <=> y= (80-5x)/6.
Pour la question 3)c):
On pose 40/x=(80-5x)/6 et 60/x=(80-5x)/6.
Pour une satisfaction de 300:
60/x=(80-5x)/6 <=> -5x²+80x-360=0 , on trouve delta=-800, il n'y a pas de solution, donc sous la contrainte budgétaire de ce consommateur, on ne peut pas avoir une satisfactin égale à 300. (La courbe est toujours située au dessus de la droite).
Pour une satisfaction de 200:
40/x=(80-5x)/6 <=> -5x²+80x-240=0, on trouve delta=1600, il y a deux solutions x1=(-80-40)/(2*-5)=12 et x2=4
On calcule y1=10/3 et y2=10; il y a donc deux points d'intersections entre la courbe y=40/x et la droite y=(80-5x)/6: Les points A(4;10) et B(12;10/3).
Donc là je dit que, oui, on peut avoir une satisfation égale à 200 sous la contrainte budgétaire de ce consommateur, pour tout les points situés sur la courbe de niveau 200, avec x compris entre 4 et 12 ?
Merci de votre je pensais ne jamais y parvenir 
Juste une dernière question, lorsque je représente la carte des courbes, comme x et y sont des produits, je ne représente les courbes que pour x>0 et y>0, ou pour tout x et y ?
Encore merci
C'est parfait !
... et merci d'avoir soulevé la faute (de frappe, tu t'en doutes bien).
Comme il s'agit d'hyperboles, il est bien question de .
Concernant ta dernière question, il faut en effet restreindre le graphique aux valeurs positives de x et y, puisque x et y représentent les quantités de biens A et B.
Voici pour la visualisation de la question 3c).
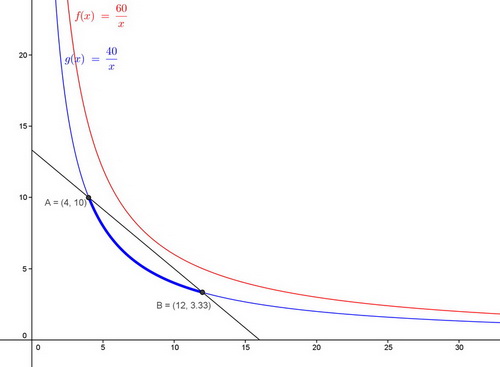
Merci de votre aide, je viens de terminer le DM, et merci également d'avoir pris le temps de tracer le graphique 
Bonne soirée.


